срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста срочно пожалуйста
Приложения:
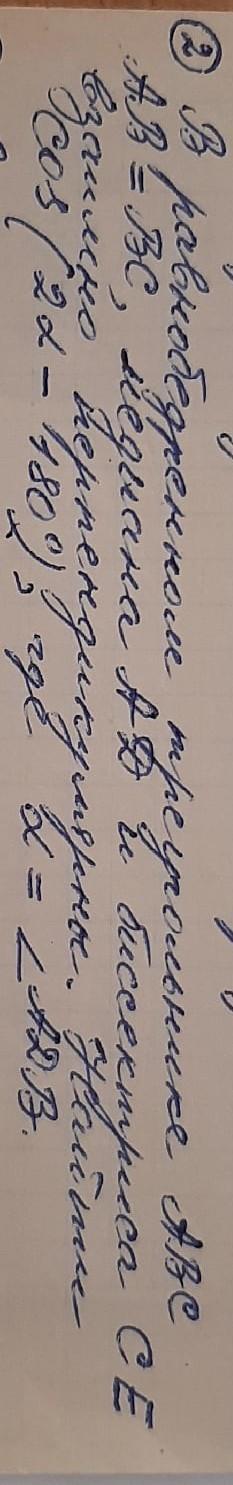
Ответы на вопрос
Ответил sarvishosho
0
Пошаговое объяснение:
Решение
Обозначим CD = DB = a, ∠C = α < 90°. Пусть P – точка пересечения биссектрисы CE и медианы AD. Тогда биссектриса CP треугольника ACD является его высотой. Поэтому треугольник ACD – равнобедренный, AC = CD = a.
Если BM – высота треугольника ABC, то cos α = MC/BC = ¼, sin α/2 = под корнем 1-cosa дробная черта, снизу 2= под корнем 6 дробная черта, снизу 4
Следовательно, cos∠ADB = cos(90° + α/2) = – sin α/2 = под корнем 6 дробная черта, снизу 4
Ответ: 180° – arccos под корнем 6 дробная черта, снизу 4 .
Надеюсь правильно..
Новые вопросы
Английский язык,
1 год назад
Окружающий мир,
1 год назад
Математика,
2 года назад
Математика,
2 года назад
Алгебра,
7 лет назад