Срочно пожалуйста срочно нужно
Приложения:
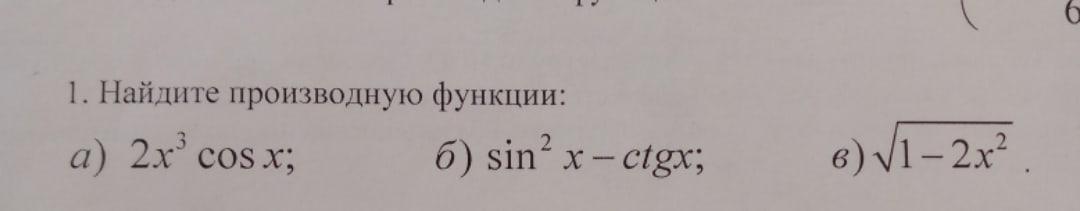
Ответы на вопрос
Ответил Miroslava227
1
Ответ:
а
б
в
Новые вопросы
Математика,
1 год назад
Алгебра,
1 год назад
Алгебра,
6 лет назад
Физика,
6 лет назад
Математика,
8 лет назад