Математика, вопрос задал ktchup , 6 лет назад

СРОЧНО ПОЖАЛУЙСТА!!!!

Приложения:

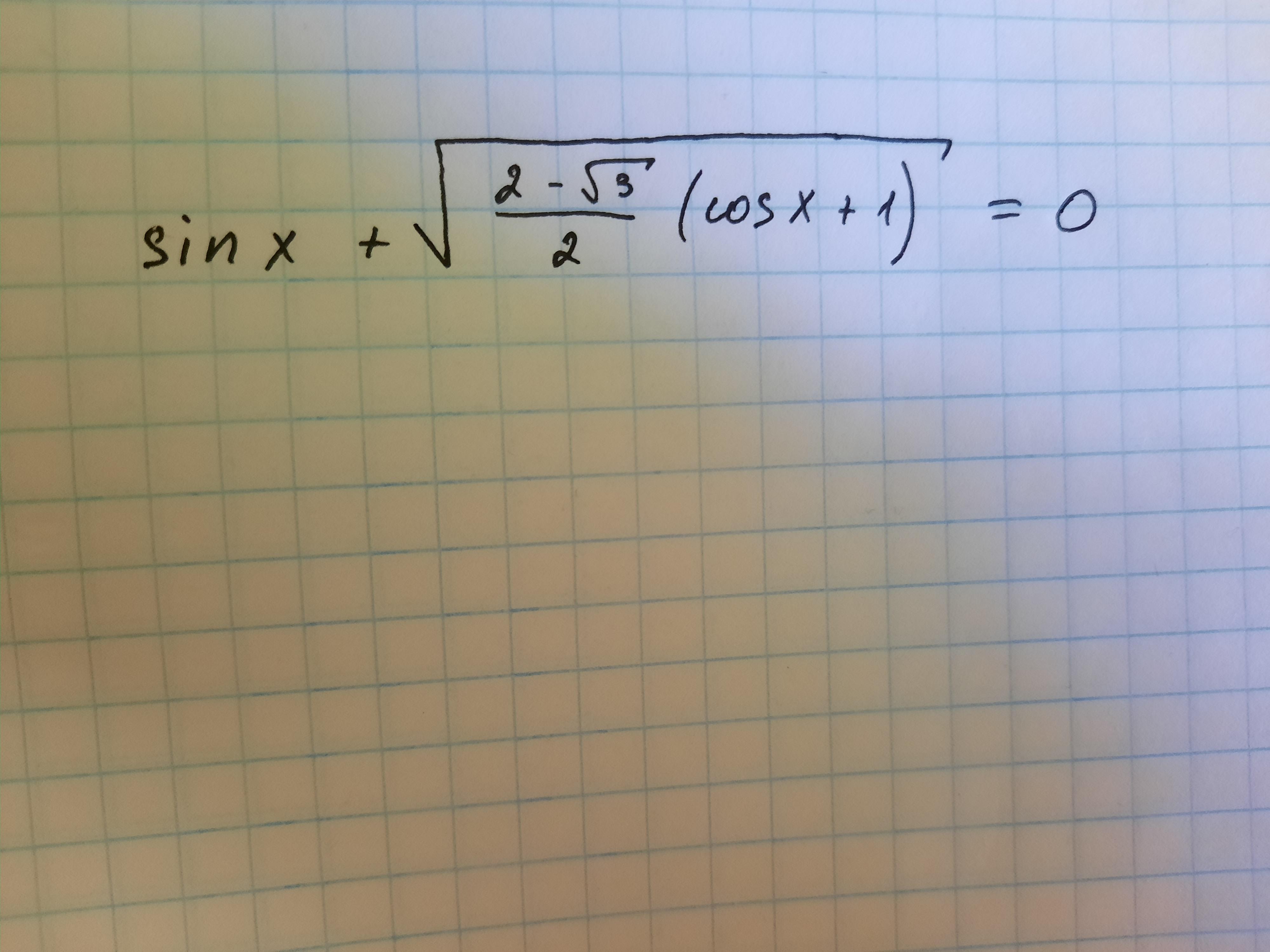
Ответы на вопрос

Ответил kamilmatematik100504

Ответ: 330

Пошаговое объяснение:

$sinx+\sqrt{\frac{2-\sqrt{3} }{2} (cosx+1)}=0$ ; $\frac{2-\sqrt{3} }{2} =1-cos30$ ; => $sinx+\sqrt{(1-cos30)(1+cosx) }$ =0 так как cos положительный только в I и в IV четверти то x ∈(0;90) и (270;360) ; значение sinx должно быть отрицательным поэтому берем III и IV четверть можно заметить что и у синуса и косинуса совпадет IV четверть тогда x ∈ (270;360) теперь решим упрощенное уравнение $sin^2x=(-\sqrt{(1-cos30)(1+cosx) })^2$ ; формула $sin^2x=1-cos^2x$ => $1-cos^2x=(1-cos30)(1+cosx)$ $(1-cosx)(1+cosx)=(1+cosx) (1-cos30)$ $1-cosx=1-cos30$ так как x в промежутке (270;360) то x=330 что верно p.s я закончил 7 класс :)