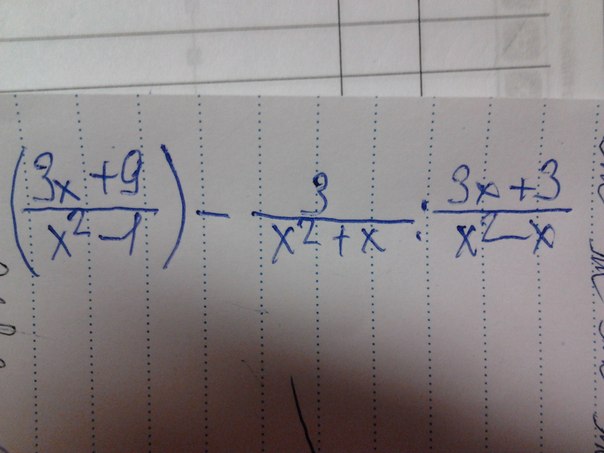
Алгебра, вопрос задал chubyr93 , 9 лет назад

Срочно помогите!!!!Даю 20 балов!!!

Приложения:

Ответы на вопрос

Ответил Anastsiia

$= frac{3x+9}{(x-1)(x+1)}- frac{3}{x(x+1)}: frac{3(x+1)}{x(x-1)}= frac{3x+9}{(x-1)(x+1)}- frac{3}{x(x+1)}*frac{x(x-1)}{3(x+1)}= \ = frac{3x+9}{(x-1)(x+1)}- frac{x-1}{(x+1)(x+1)}= frac{(3x+9)(x+1)-(x-1)(x-1)}{(x-1)(x+1)(x+1)}= \ = frac{3 x^{2} +3x+9x+9- x^{2} +2x-1}{(x-1)(x+1)(x+1)} = frac{2 x^{2} +14x+8}{(x-1)(x+1)(x+1)}$

Cкорее, условие было такое, что разница дробей в скобках, а потом уже деление на последнюю дробь.

$= (frac{3x+9}{(x-1)(x+1)}- frac{3}{x(x+1)}): frac{3(x+1)}{x(x-1)}= (frac{3x+9}{(x-1)(x+1)}- frac{3}{x(x+1)})*frac{x(x-1)}{3(x+1)}= \ = frac{(3x+9)x-3(x-1)}{x(x-1)(x+1)}* frac{x(x-1)}{3(x+1)}= frac{3 x^{2} +9x-3x+3}{x+1}* frac{1}{3(x+1)} = \ = frac{3 (x^{2} +2x+1)}{x+1}* frac{1}{3(x+1)}= frac{(x+1)^2}{x+1}* frac{1}{(x+1)}=1$

Приложения:

Предыдущий вопрос

Следующий вопрос

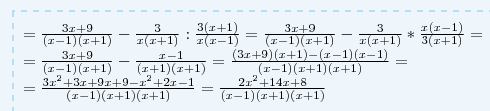
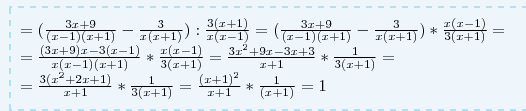
Новые вопросы

Математика, 2 года назад

14(х+47)=0 Розвяжіть рівняння...

Английский язык, 2 года назад

Read these sentences and identify the tense: Future Simple or Future Continuous. 1. Jack will be dancing with three girls all evening. Future Continuous Future Simple 2. It will be raining.

Математика, 9 лет назад

До остановки автобуса папа идёт 10 минут,а на автобусе едет на работу на 20 минут больше,чем идёт до остановки.Сколько всего времени он тратит на дорогу? Решить задачу с кратким условием.

Алгебра, 9 лет назад

Помогите решить уравнения!!! Срочно нужно!!! Фотографии заданий в приложении...

Математика, 9 лет назад

Коля, Дима и Саша собрали вместе 30 грибов. Дима нашел в 2 раза больше грибов,чем Коля, а Коля- в 3 раза меньше чем Саша. Сколько грибов нашёл каждый из них?

Математика, 9 лет назад

Определите закон, по которому записаны эти цифры: 8,2,9,0,1,5,7,3,4,6.