Срочно ОКР помагите по математике
Приложения:
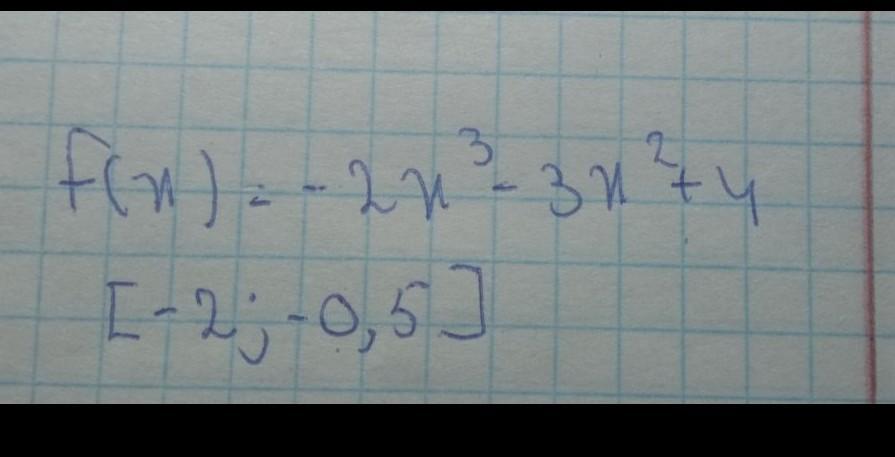
Ответы на вопрос
Ответил daraprelj
1
Ответ:
f(-1) = 3 - точка минимума
Пошаговое объяснение:
Рассмотрим координатную прямую(все точки закрашены)
- +
---------------₀-------------------₀-------->
↓ -1 ↑ 0 x
f'(-2) = -6*(-2)*(-2+1) = 12*(-1) = -12 < 0
f'(-0,5) = -6*(-0,5)*(-0,5+1) = 3*0,5 = 1,5 > 0
Из рисунка видно, что точка х = -1 - это точка минимума
f(-1) = -2*(-1)³-3*(-1)²+4 = -2*(-1)-3*1+4 = 2-3+4 = 3
v4443376:
Спасибо огромное
поможешь ещё с одним вопросом?
Новые вопросы