Алгебра, вопрос задал kei5 , 2 года назад

СРОЧНО, нужно найти значение выражения. ДАЮ 30 БАЛЛОВ.

Приложения:

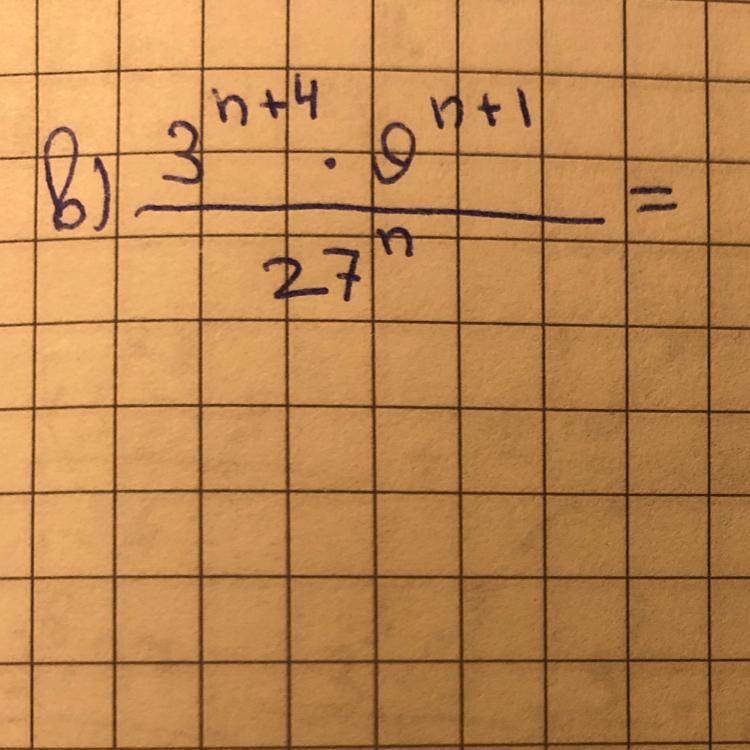
Ответы на вопрос

Ответил papagenius

Решение и ответ:

$\displaystyle \frac{{{3^{n+4}}\cdot{9^{n+1}}}}{{{{27}^n}}}=\frac{{{3^{n+4}}\cdot{3^{2(n+1)}}}}{{3^{3n}}}=\frac{{{3^{n+4}}\cdot{3^{2n+2}}}}{{3^{3n}}}=$

$\displaystyle =\frac{{{3^{n+4+2n+2}}}}{{{3^{3n}}}}=\frac{{{3^{3n+6}}}}{{{3^{3n}}}}={3^{3n+6-3n}}={3^6}=\boxed{729}$

kei5: спасибо большое!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

СРОЧНООООО!!! Определите спр. гл., образуйте форму 3 лица, мн. ч. и дейст. причастие, наст. времени °Колыхать Зависеть, хлопотать, дышать, рокотать, строить, терпеть, тараторить, гнать..

Беларуская мова, 1 год назад

вызначце ў словах націскные склады.З націскных складоў састаўце новые словы. 1Маліны,рамонкі.2Рака,шафа.3Маша,Мілана,Коля.

Математика, 2 года назад

2) Сколько трёхзначных чисел одновременно делятся на 3 и 8, но не делится на 16?

Английский язык, 2 года назад

помогите пж срочно надо завтра задавать ...

Алгебра, 7 лет назад

Помогите решить используя введение новой перемннной...

Алгебра, 7 лет назад

Решите неравенство 1,3x-2<2x-0,6...