СРочно нужна помощь в решении

Ответ:

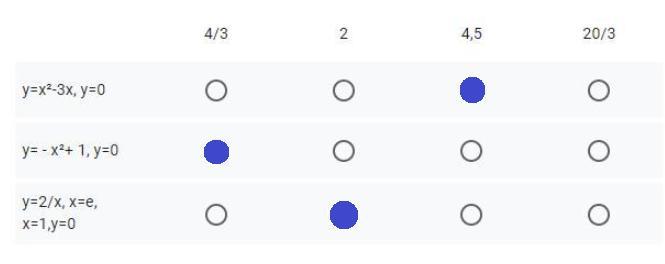
1) 4.5

2) 4/3

3) 2

Объяснение:

площадь для первой фигуры интеграл от нуля до трех от функции

(0-(х²-3х))=3х-х²,  равна (3*3²/2-3³/3) -(3*0²/2-0³/3)=13.5-9-0=4.5- ответ третий, здесь первообразная от указанной функции равна 3х²/2-х³/3, а пределы нашел из условия х²-3х=0, х*(х-3)=0; х=0; х=3.

2)1-х²=0, х=±1, т.е. пределы интегрирования от -1 до 1, от функции (1-х²-0), первообразная равна х-х³/3, по формуле Ньютона - Лейбница определенный интеграл равен площади искомой  1-1³/3-( -1-(-1)³/3)=

1-1/3+1-1/3=2-2/3=4/3- это первый ответ

3) площадь равна определенному интегралу от 1 до е от функции

(2/х-0)=2/х, ее первообразная 2㏑IxI, значит, площадь

2㏑IеI-2㏑I1I=2*1-0=2- второй ответ