СРОЧНО!
Фото РЕШЕНИЕ
Приложения:
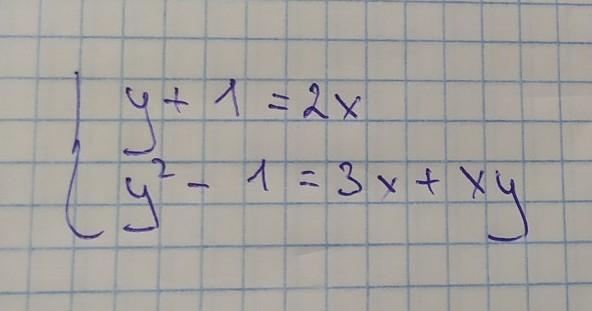
Ответы на вопрос
Ответил Universalka
2
Новые вопросы
Русский язык,
1 год назад
Химия,
6 лет назад