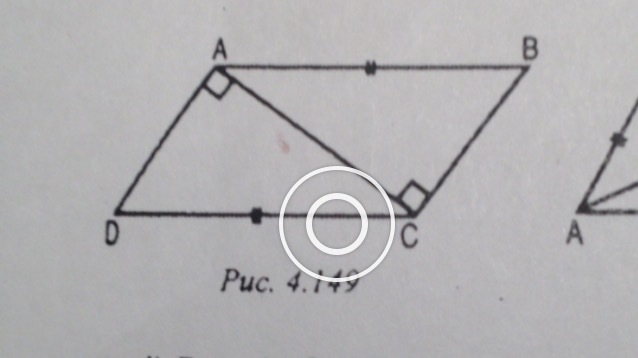
Срочно. Доказать ABC = CDA
Приложения:
Ответы на вопрос
Ответил grigorijsvetov
0
Боюсь, что это решение больше подойдет для разбора... И не знаю, можно ли применять теорему Пифагора...
Потому что вообще, если это всё в условии, то самый простой способ - через теорему Пифагора (доказав тем самым признак равенства прямоугольных треугольников по гипотенузе и катету).
Пусть имеются два прямоугольных треугольника: ABC, DEF (прямыми являются углы B и E).
Пусть катеты EF и BC равны между собой и равны некоей a.
Пусть гипотенузы AC и DF равны между собой и равны некоей с.
Тогда катеты AB и DE также равны между собой и равный некоей
 (по теореме Пифагора)
(по теореме Пифагора)
Треугольники равны по общему третьему признаку равенства треугольников.
Следовательно, если два катета и две гипотенузы попарно равны, то прямоугольные треугольники также равны. Назовем это признаком равенства прямогугольных треугольников по гипотенузе и катету.
В нашей задаче AC - общий катет (AC=AC). DC=AB (и это гипотенузы). По признаку равенства прямогугольных треугольников по гипотенузе и катету мы доказали, что ABC = CDA.
Потому что вообще, если это всё в условии, то самый простой способ - через теорему Пифагора (доказав тем самым признак равенства прямоугольных треугольников по гипотенузе и катету).
Пусть имеются два прямоугольных треугольника: ABC, DEF (прямыми являются углы B и E).
Пусть катеты EF и BC равны между собой и равны некоей a.
Пусть гипотенузы AC и DF равны между собой и равны некоей с.
Тогда катеты AB и DE также равны между собой и равный некоей
Треугольники равны по общему третьему признаку равенства треугольников.
Следовательно, если два катета и две гипотенузы попарно равны, то прямоугольные треугольники также равны. Назовем это признаком равенства прямогугольных треугольников по гипотенузе и катету.
В нашей задаче AC - общий катет (AC=AC). DC=AB (и это гипотенузы). По признаку равенства прямогугольных треугольников по гипотенузе и катету мы доказали, что ABC = CDA.
Ответил marshal500
0
ABC = CDA по двум сторонам (DC=AB, AC общая) и углу 90°.
Новые вопросы
Математика,
2 года назад
Русский язык,
2 года назад
Алгебра,
8 лет назад
Литература,
8 лет назад
Математика,
9 лет назад
История,
9 лет назад