Алгебра, вопрос задал vv12789vv , 6 лет назад

Срочно ! Даю 50 балов !

Приложения:

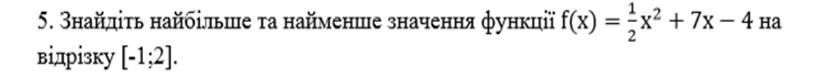
Ответы на вопрос

Ответил Universalka

$\displaystyle\bf\\f(x)=\frac{1}{2} x^{2} +7x-4$

Найдём производную :

$\displaystyle\bf\\f'(x)=\frac{1}{2} \cdot(x^{2} )'+7\cdot x'-4'=\frac{1}{2} \cdot2x+7\cdot 1-0=x+7$

Приравняем производную к нулю , найдём критическую точку :

$\displaystyle\bf\\f'(x)=0\\\\x+7=0\\\\x=-7$

Эта точка не принадлежит отрезку [ - 1 ; 2] , поэтому найдём значения функции только на концах отрезка и сравним их .

$\displaystyle\bf\\f(-1)=\frac{1}{2} \cdot (-1)^{2} +7\cdot(-1)-4=\frac{1}{2} -7-4=-10,5\\\\f(2)=\frac{1}{2} \cdot 2^{2} +7\cdot 2-4=2+14-4=12$

Наименьшее значение функции равно - 10,5 , а наибольшее значение равно 12 .

Новые вопросы

Другие предметы, 1 год назад

Русский язык, 1 год назад

Алгебра, 6 лет назад

Обществознание, 6 лет назад

Математика, 8 лет назад

Математика, 8 лет назад