СРОЧНО, ДАЮ 30 БАЛЛОВ !!!!
Это алгебра!

Ответ:

1. Ответ: Г. -3³

2. Ответ: А.  (a + b)² > a² + b²

3. Ответ: А.

Объяснение:

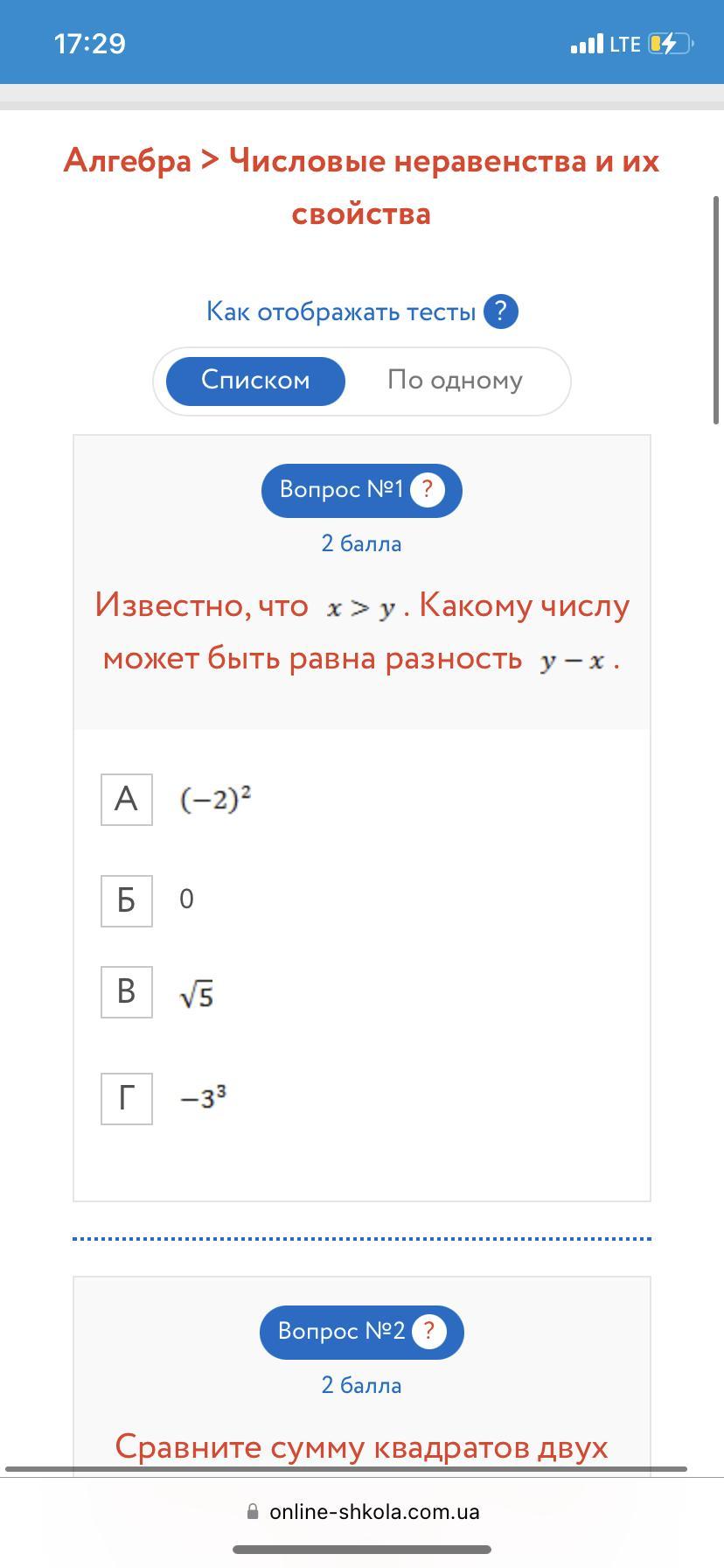
1. Известно, что x > y. Какому числу может быть равна разность у - х?

x > y

• Любое слагаемое можно переносить из одной части неравенства в другую, поменяв знак на противоположный.

0 > y - x

или

у - х < 0

То есть разность отрицательна.

А. (-2)² = 4 > 0 - не подходит

Б. 0 - не подходит

В. √5 > 0 - не подходит

Г. -3³ = -27 - подходит.

Ответ: Г. -3³

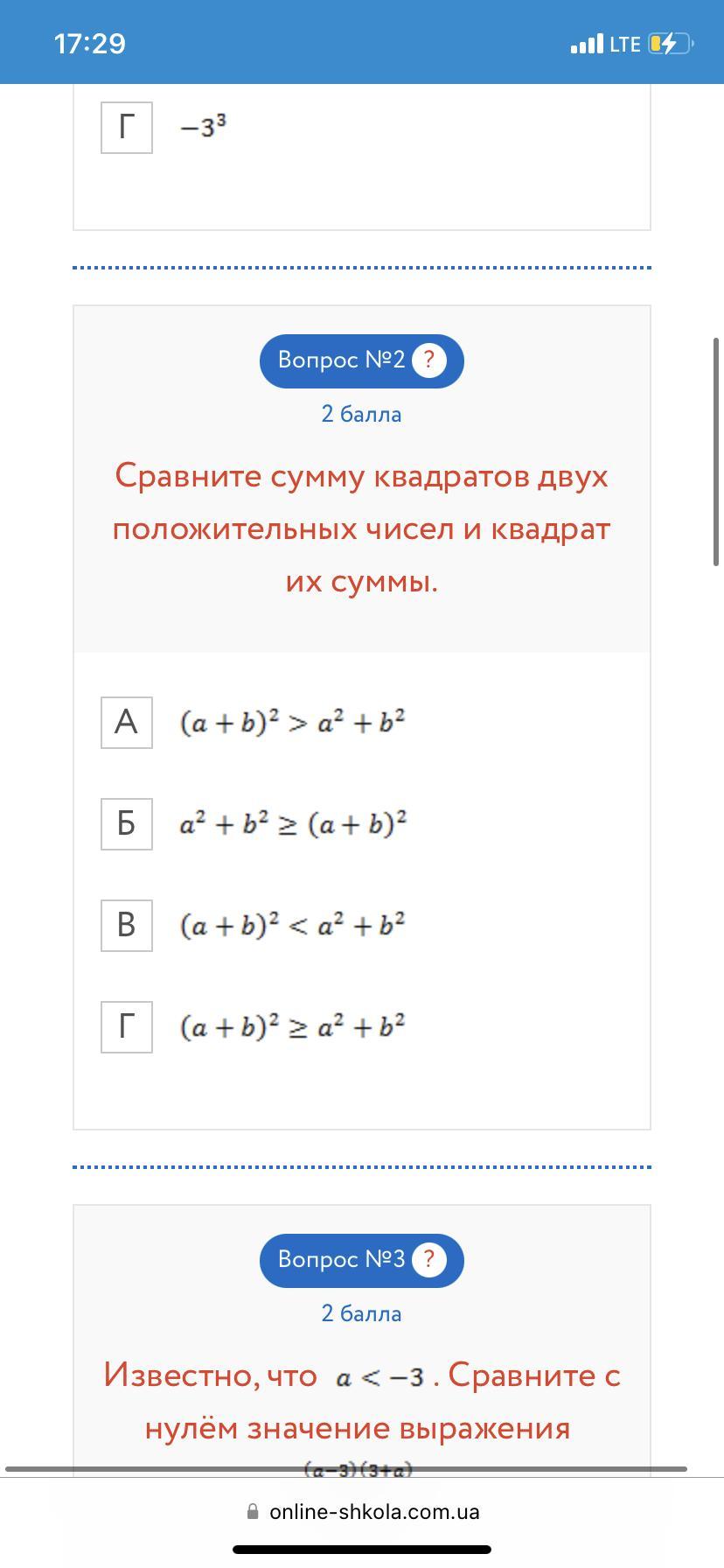
2. Сравните сумму квадратов двух положительных чисел и квадрат их суммы.

Сравним (a + b)² и a² + b²

Разложим по формуле:

(a + b)² = a² + 2ab + b² = (a² + b²) + 2ab

Видим, что квадрат суммы больше суммы квадрата на выражение 2ab.

(a² + b²) + 2ab > a² + b²

⇒ (a + b)² > a² + b²

Ответ: А.  (a + b)² > a² + b²

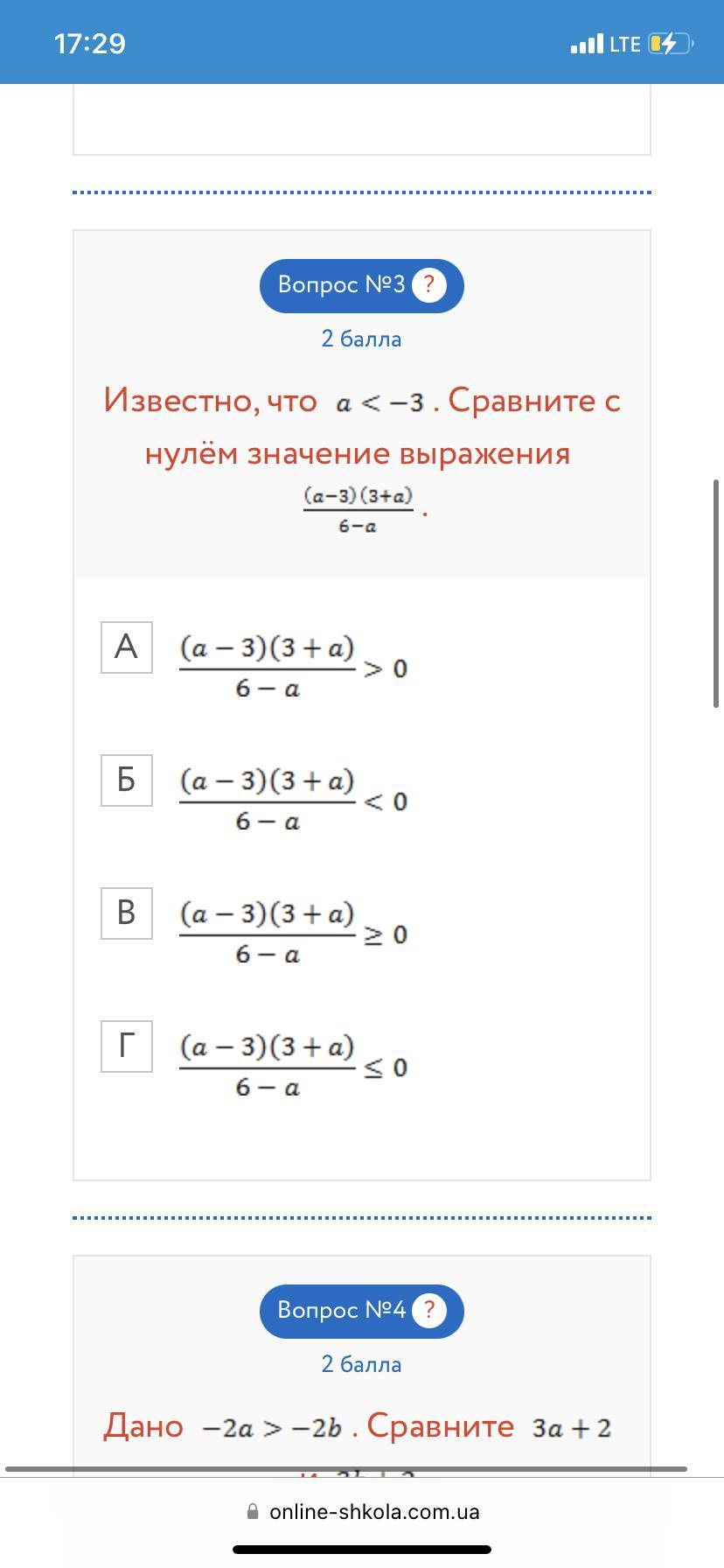
3. Известно, что а < - 3. Сравните с нулем значение выражения

Возьмем любое число меньше (-3) и подставим в данное выражение. Нам нужен только знак полученного результата.

Например, число (-4). Получим:

Ответ: А.

#SPJ1