СРОЧНО!ДАЮ 100 БАЛЛОВ!!!
На сторонах АВ и СD параллелограмма АВСD
взяли точки М и К так, что АМ = СК. Докажите, что
отрезок МК проходит через точку пересечения
диагоналей параллелограмма.

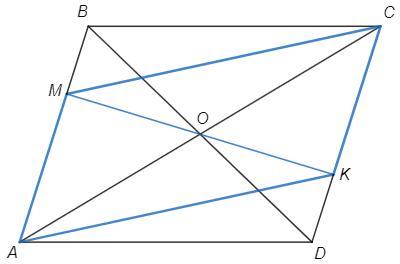
Дано: ABCD - параллелограмм; M на AB, K на CD; AM=CK

Доказать, что MK проходит через точку пересечения диагоналей ABCD.

Диагонали параллелограмма точкой пересечения делятся пополам. Пусть O - середина диагонали AC. Тогда по свойству параллелограмма диагонали AC и BD пересекаются в точке O.

Противоположные стороны параллелограмма параллельны (AB||CD), следовательно отрезки AM и CK параллельны. Если в четырехугольнике противоположные стороны параллельны и равны, то он является параллелограммом.

AM||CK, AM=CK => AMCK - параллелограмм (по признаку)

По свойству параллелограмма (AMCK) диагональ MK проходит через середину диагонали AC, то есть через точку O.