срочно, даю 100 баллов
Приложения:
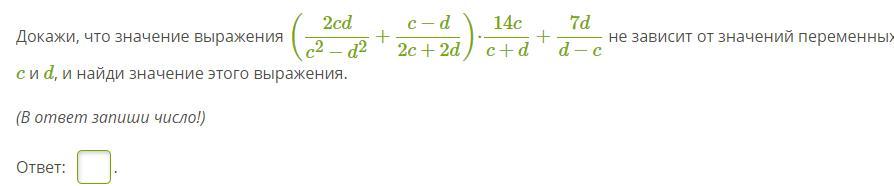
vladlyashko:
Добрый день! Можно "лучший ответ"(корону), пожалуйста?
Ответы на вопрос
Ответил vladlyashko
0
Ответ:
0
Пошаговое объяснение:
Первым действием выполним сложение в скобках:
Общий знаменатель - 2 * (c - d)(c + d):
Сократим числитель и знаменатель на (c + d):
Умножим получившееся значение на :
И, наконец прибавим к этому выражению . Общий знаменатель у них - (c - d), значит числитель и знаменатель выражения
на -1:
Это значит, что при любых значениях с и d выражение будет равно 0, а следовательно, оно не зависит от переменных c и d.
Новые вопросы
История,
6 лет назад
Математика,
8 лет назад