СРОЧНО!
Дано: cos a=0,8, cos B= -12/13
270° ∠a ∠360°, 180° ∠B ∠270°
Знайти: sin (a, B)
Приложения:
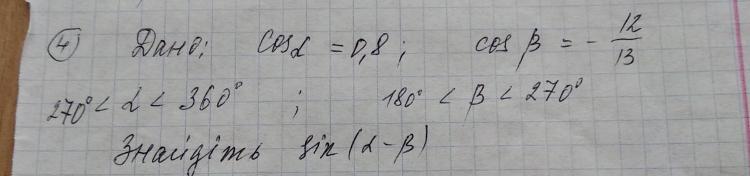
Ответы на вопрос
Ответил Dazami
1
cos²(a) + sin²(a) = 1
sin²(a) = 1 - cos²(a)
sin(a) = √(1-0,8²) = √0,36
т. к. 270<а<360 (угол 4 четверти), то синус отрицательный
sin(a) = - 0,6
cos²β + sin²β = 1
sinβ = √(1 - cos²β) = √(1 - 144/169) = √25/169
Т.к. 180<β<270 (угол 3 четверти), то синус отрицательный
sinβ = -5/13
sin(a-β) = sin(a)·cos(β) - sin(β)·cos(a) = - 0,6 * (-12/13) - (-5/13)*0,8 = 36/65 + 4/13 = 56/65
vika51234:
Спасибо большое
❤️
Новые вопросы