СРОЧНО БЛАГАЮ. Розв'язати рівняння: (2х-8)/х-5 - (х-4)/х+5 = -10/х^2-25
Приложения:
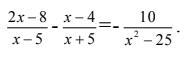
Ответы на вопрос
Ответил hodos45anton
1
Спочатку застосуємо спільний знаменник для перших двох дробів:
(2x - 8)/(x - 5) - (x - 4)/(x + 5) = -10/(x^2 - 25)
[(2x - 8)(x + 5) - (x - 4)(x - 5)] / (x^2 - 25) = -10 / (x^2 - 25)
Виконаємо залишок множення для нумератора лівої дробу:
(2x^2 + 2x - 40) - (x^2 - 9) = -10
Розкриємо дужки та скоротимо подібні члени:
x^2 + 2x - 31 = 0
Застосуємо квадратне рівняння:
x = (-2 ± √(2^2 - 4*1*(-31))) / (2*1)
x₁ = -5.1, x₂ = 3.1
Відповідь: x₁ = -5.1, x₂ = 3.1.
Новые вопросы
Химия,
11 месяцев назад
Английский язык,
11 месяцев назад
Математика,
1 год назад
Математика,
1 год назад
Химия,
6 лет назад