Алгебра, вопрос задал MissFelton22 , 8 месяцев назад

срочно . . . . . . .. .

Приложения:

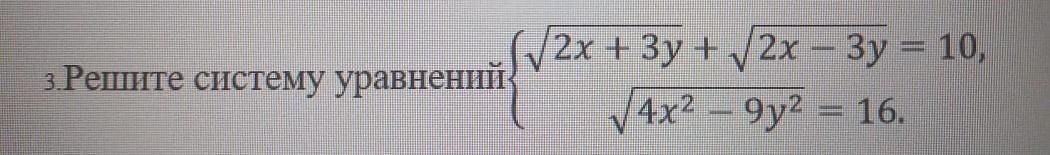
Ответы на вопрос

Ответил laska0646425

1

Объяснение:

см фото ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

Приложения:

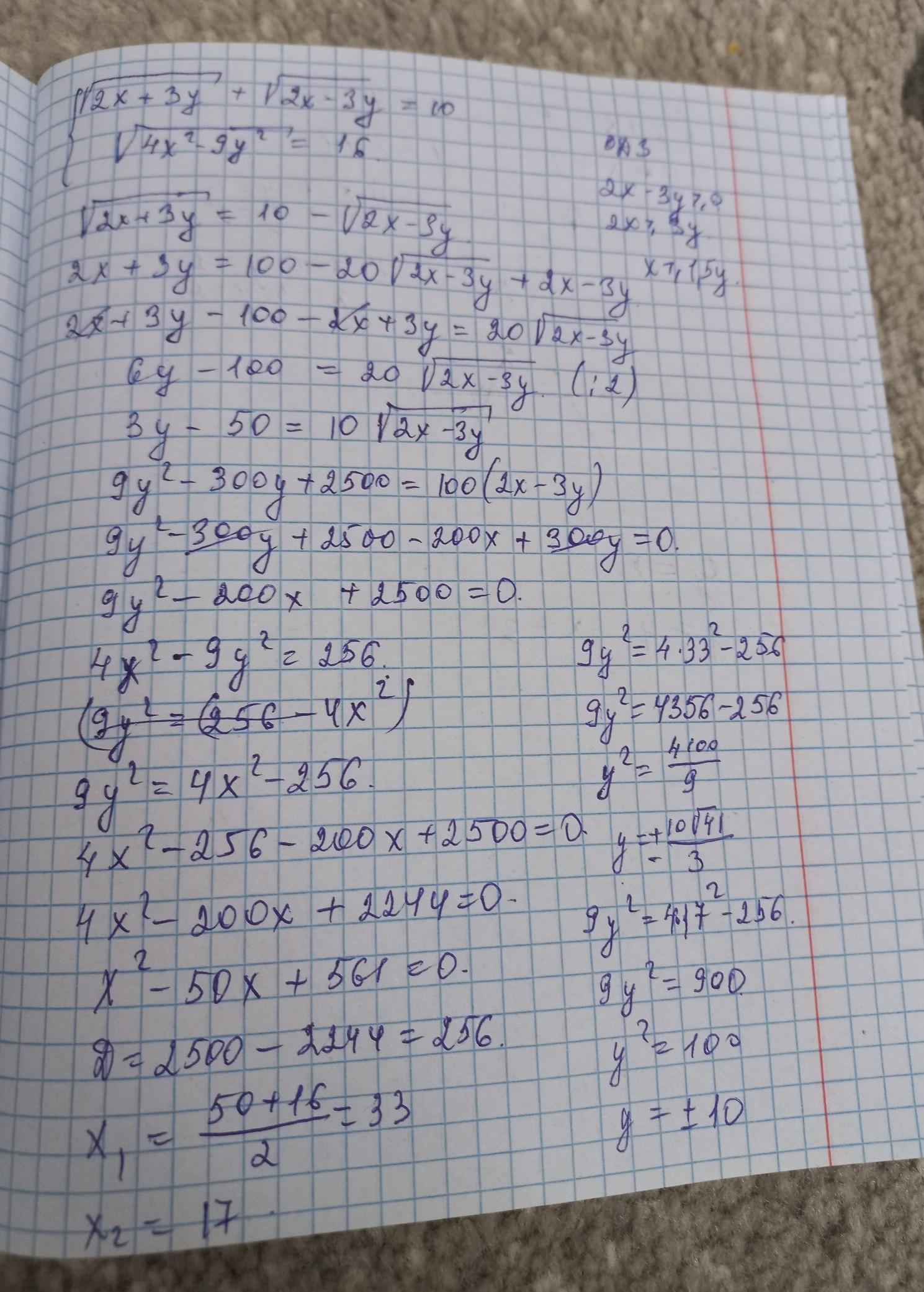
polarkat: Решение как будто с калькулятора какого-то

laska0646425: А что не так?

Ответил polarkat

2

$\begin{cases}\sqrt{2x+3y}=a,a\geq 0\\ \sqrt{2x-3y}=b,b\geq 0\end{cases}\Rightarrow \begin{cases}a+b=10\\ ab=16\end{cases}\Leftrightarrow \begin{cases}a=10-b\\ (10-b)b=16\end{cases}\\\\b^2-10b+16=0\\D_b=100-64=36\Rightarrow b=\cfrac{10\pm\sqrt{36}}{2}=\left \{ 2,8 \right \}\\b=2\Rightarrow 2a=16\Rightarrow a=8\\b=8\Rightarrow 8a=16\Rightarrow a=2$

$\begin{cases}\sqrt{2x+3y}=2\\ \sqrt{2x-3y}=8\end{cases}\Leftrightarrow \begin{cases}2x+3y=4\\ 2x-3y=64\end{cases}\Rightarrow 4x=68\Rightarrow x=17\\x=17\Rightarrow 2\cdot 17+3y=4\Leftrightarrow 34+3y=4\Rightarrow 3y=-30\Rightarrow y=-10\\x=17\Rightarrow 2\cdot 17-3y=4\Leftrightarrow 34-3y=4\Rightarrow -3y=-30\Rightarrow y=10$

Нет смысла рассматривать второй случай, так как он симметричный. Ответ $(x,y)=(17,\pm 10)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

География, 5 месяцев назад

СРОЧНО! Допоможіть. які атмосферні процеси визначають погоду в Україні в останні дні. Обґрунтуйте прогноз погоди у вашій місцевості на завтрашній день...

Другие предметы, 5 месяцев назад

Луна легче Земли а) в 15 раз, б) в 81 раз, в) в 120 раз...

Английский язык, 8 месяцев назад

Нужен диолог на английском!! С продовцом...

Физика, 8 месяцев назад

(+5q+(-13q))/2 решите пожалуйста очень нужно...

Математика, 6 лет назад

Найдите косинус углов между векторами a и, если a(5√3;5) и b(5√3;-5)...

Обществознание, 6 лет назад

СРОЧНО!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Вредные и полезные привычки: каких у меня больше?