Срочно 40балов дам пожалуйста
Ответы на вопрос
Ответ:
120°
Объяснение:
1) Угол между двумя пересекающимися касательными к окружности равен 180°–а, где а– градусная мера меньшей дуги, образованных точками касания
2) Градусная мера дуги равна градусной мере соответствующего центрального угла или угла, дополняющего центральный угол до 360°
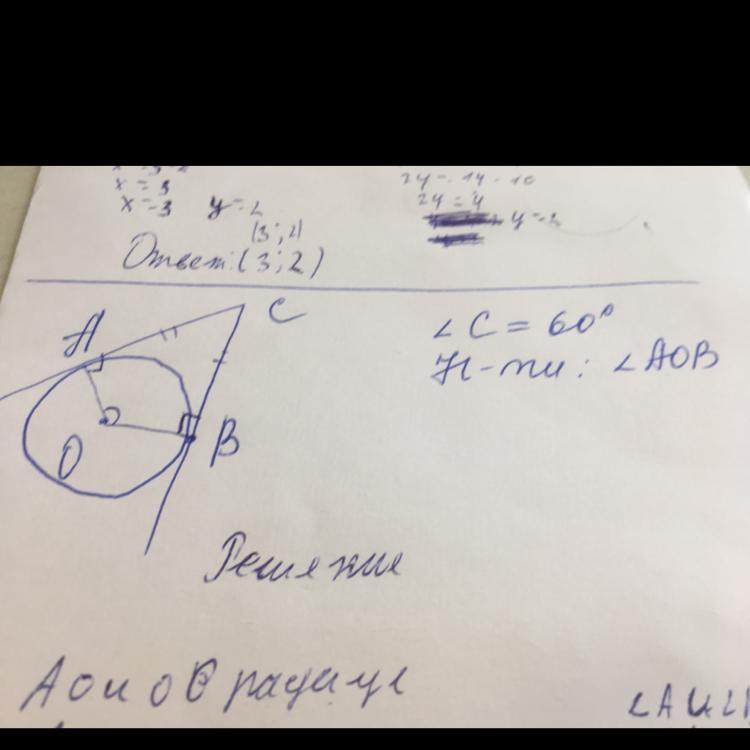
∪АВ = ∠АОВ = 180° - 60° = 120°
_________________________________
Если требуется более подробное доказательство, то так:
Соединим центр окружности О с вершиной угла С.
Теорема: Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Т.е.,
АС = СВ и ∠АСО = ∠ВСО = 60°/2 = 30°
∠САО = ∠СВО = 90° (теорема: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.)
ΔСАО = ΔВСО по трем сторонам: АС=ВС, АО =ВО как радиусы, ОС - общая сторона) или по гипотенузе и катету( АС = СВ, АО = ОВ), т.к. они прямоугольные.
Сумма углов в треугольнике = 180°, следовательно,
∠АОС = 180° - 90° - 30° = 60°, но
∠АОС = ∠ ВОС. т.к. ΔСАО = ΔВСО, тогда
∠АОВ = 60° * 2 = 120°