Математика, вопрос задал rabovaleksej37 , 1 год назад

СРОЧНО!!! 20 баллов!!!!!!!!!

Приложения:

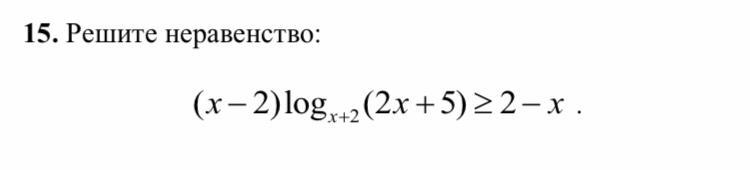
Ответы на вопрос

Ответил Аноним

1

ОДЗ:

$\left\{\begin{matrix}2x+5>0\\ x+2>0\\ x+2\neq 1 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x>-2.5\\ x>-2\\ x\neq -1 \end{matrix}\right. \Leftrightarrow x \in (-2;-1) \cup(-1;+\infty)$

Решение:

$(x-2)\log_{x+2}(2x+5)\geq 2-x \\ \\ (x-2)\log_{x+2}(2x+5)+x-2\geq 0 \\ \\ (x-2)[\log_{x+2}(2x+5)+1]\geq 0 \\ \\ (x-2)[\log_{x+2}(2x+5)+\log_{x+2}(x+2)]\geq 0 \\ \\ (x-2)\log_{x+2}[(2x+5)(x+2)]\geq 0 \\ \\ (x-2)(\log_{x+2}[(2x+5)(x+2)]-0)\geq 0 \\ \\ (x-2)(\log_{x+2}[(2x+5)(x+2)]-\log_{x+2}1)\geq 0 \\ \\ (x-2)(x+2-1)[(2x+5)(x+2)-1]\geq 0 \\ \\ (x-2)(x+1)(2x^2+4x+5x+10-1)\geq 0 \\ \\ (x-2)(x+1)(2x^2+9x+9)\geq 0 \\ \\ 1) \ x-2=0 \\ x=2 \\ \\ 2) \ x+1=0 \\ x=-1 \\ \\ 3) \ 2x^2+9x+9=0 \\ \\ D=81-4*2*9=9=3^2 \\$

$x_1=\frac{-9+3}{2*2}=- 1.5 \\ \\ x_2=\frac{-9-3}{4}=-3 \\ \\ +++[-3]---[-1.5]+++[-1]---[2]+++>_x$

С учетом ОДЗ:

$x \in [-1.5;-1) \cup [2;+\infty)$

$OTBET: \ x \in [-1.5;-1) \cup [2;+\infty)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

Обчислити довжину кола радиусом 6.2 м...

Математика, 1 год назад

How will $105 be shared between Jack, Ken and Aaron; if Jack gets double of what Ken gets, and Ken gets double of what Aaron gets?

Математика, 1 год назад

Сравните дроби. 1)0,25 и 3/4 2)0,5 и 1/4 3)5/6 и 0,4 4)0,6 и 4/5 5)0,7 и 73/100 6)0,2 И 9/50 Помогите пожалуйста.

Русский язык, 1 год назад

Поиграй с одноклассниками.Подбери к словосочетаниям...

Алгебра, 6 лет назад

Найдите квадратный корень комплексного числа 2i...

Математика, 6 лет назад

Как изменится дробь, если ее числитель и знаменатель увеличить в 5 раз? увеличится в 25 раз не изменится уменьшится в 10 раз уменьшится в 25 раз уменьшится в 5 раз увеличится в 10 раз...