Математика, вопрос задал Лена148 , 2 года назад

Срочно!1)Найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.
C подробным решением

Приложения:

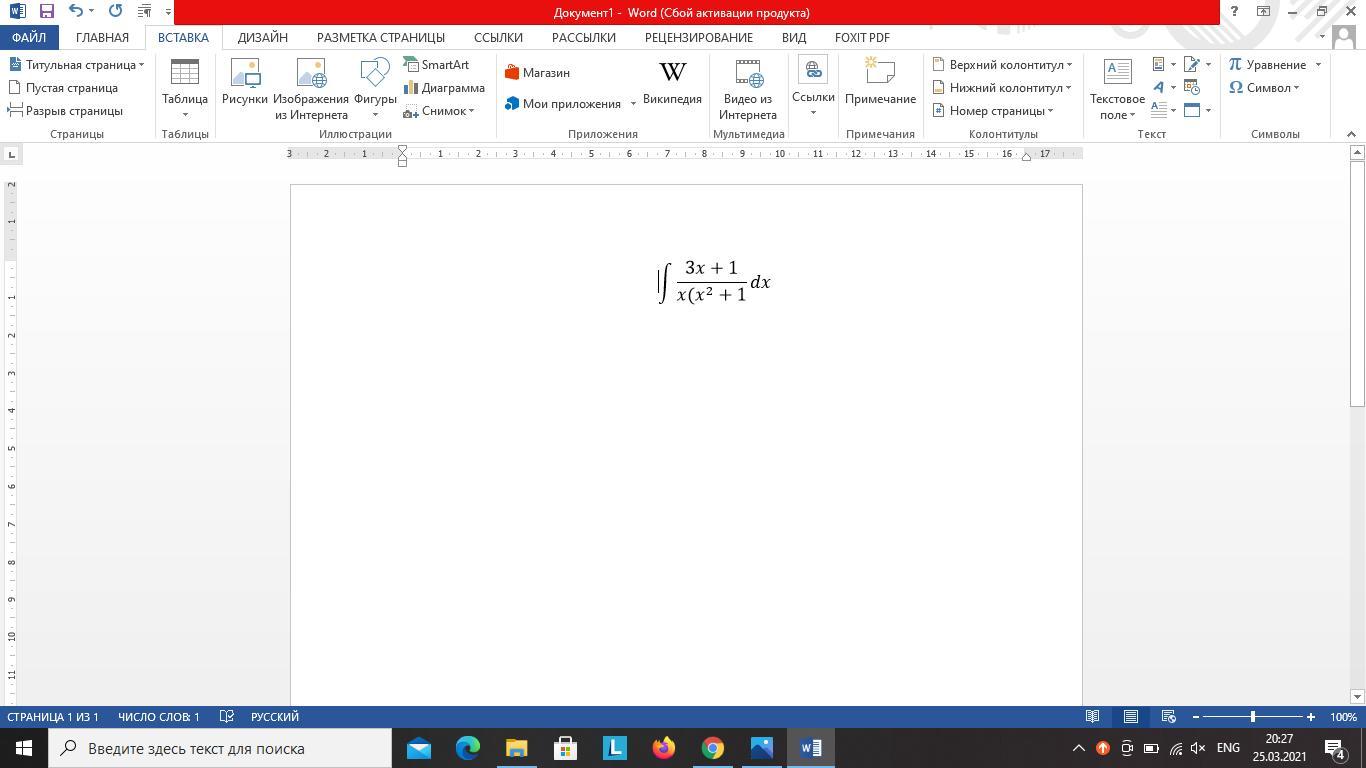
Ответы на вопрос

Ответил Miroslava227

2

Ответ:

$\int\limits \frac{3x + 1}{x( {x}^{2} + 1)} dx \\ \\ \frac{3x + 1}{ { x({x}^{2} + 1) }^{2} } = \frac{A}{x} + \frac{Bx + C}{ {x}^{2} + 1 } \\ 3x + 1 =A ( {x}^{2} + 1) + (Bx + C)x \\ 3x + 1 =A {x}^{2} + A+ B{x}^{2} + Cx \\ \\ \text{Система(левую часть приравниваем к правой)} \\ \\0 = A + B \\3 = C \\ 1 = A \\ \\ A= 1 \\C = 3 \\ B = - 1 \\ \\ \int\limits \frac{1 \times dx}{x} + \int\limits \frac{ ( - x + 3)}{ {x}^{2} + 1 }dx = \\ = ln |x| - \int\limits \frac{xdx}{ {x}^{2} + 1} + \int\limits \frac{3dx}{ {x}^{2} + 1 } = \\ = ln |x| - \frac{1}{2} \int\limits \frac{2xdx}{ {x}^{2} + 1 } + 3arctg(x) + C = \\ = ln | {x}^{} | - \frac{1}{2} \int\limits \frac{d( {x}^{2} + 1) }{ {x}^{2} + 1 } + 3arctg(x) + C = \\ = ln |x| - \frac{1}{2} ln | {x}^{2} + 1| + 3arctg(x) + C$

Приложения:

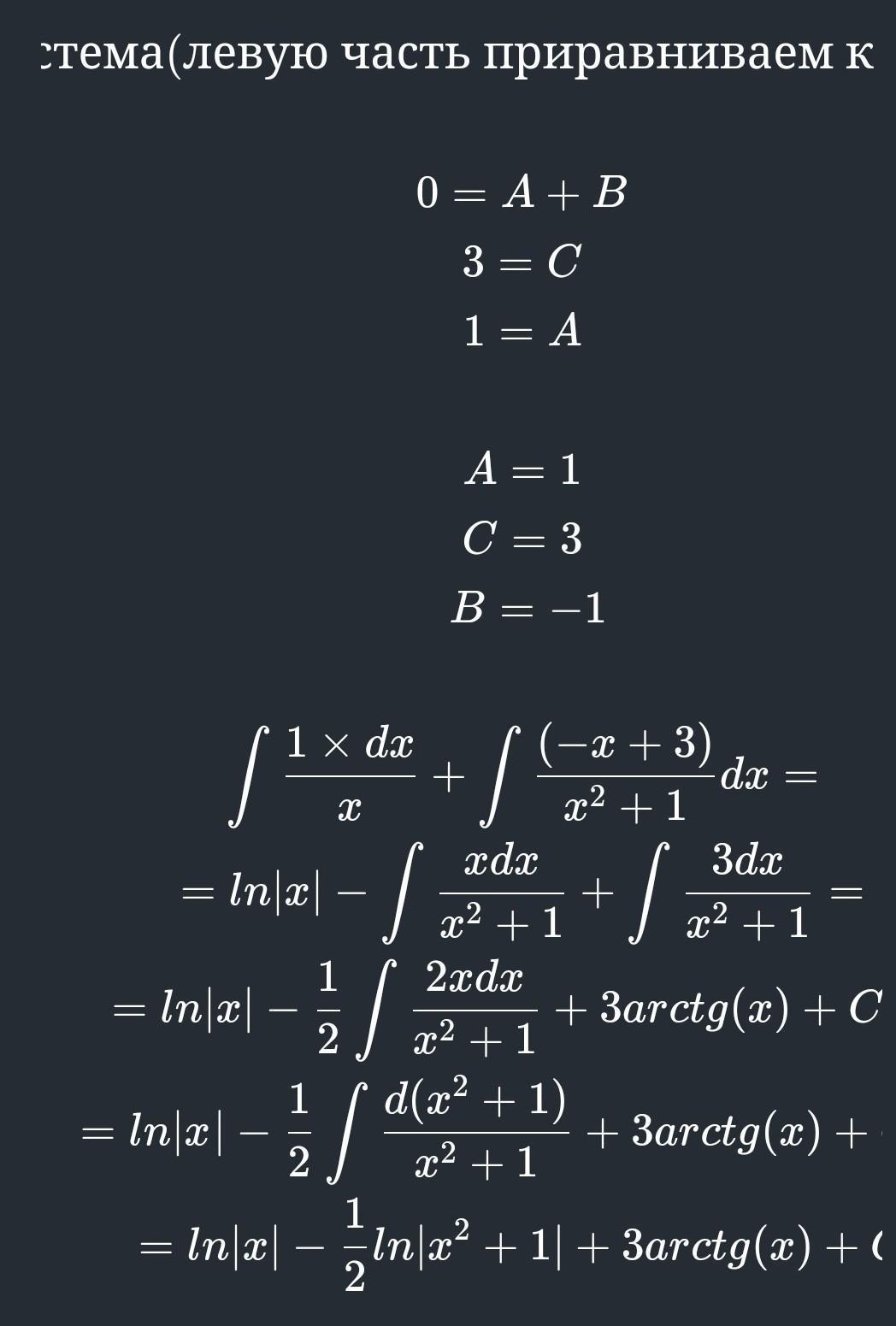
Лена148: Ответ не отображается

Лена148: можно ли ответ еще раз скинуть в правильном формате ?

Miroslava227: Посмотрите, сейчас видно?

Miroslava227: убрала значок системы

Лена148: к сожалению все по-прежнему

Лена148: если можно может фотографию ответа

Miroslava227: блин, значит с проблема конкретно на сайте

Miroslava227: с латексом

Miroslava227: загрузила скрины

Лена148: спасибо

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Окружающий мир, 1 год назад

горы расположены рядом как называются...

Русский язык, 1 год назад

что можно приписать к слову честный...

Химия, 2 года назад

2. Яка з вказаних речовин практично нерозчинна у воді: А цинк хлорид, в барій сульфат; Б магній сульфат; Галюміній нітрат.

Геометрия, 2 года назад

У прямокутному трикутнику ABC (C = 90°) провели висоту CM. Знайдіть кут ABC, якщо AC = 2 см, AM =1 см. срочно!!!

Музыка, 8 лет назад

corazon переведите с испанского...

Математика, 8 лет назад

15-8 2/5 * 1 11/24 + 3 5/6 (P.S=/ это знак дроби)...