Средние линии КМ и KN остроугольного
треугольника ABC равны соответственно 8 см и 4 см
и образуют между собой угол MKN, равный 45°.
Найдите площадь треугольника АВС.
Ответы на вопрос
Ответил АртёмПлотников
0
Площадь треугольника вычисляется по формуле: (ah)/2, то есть половина произведения основания на высоту.
Сторона AC равна 16, а сторона AB=8, так как средняя линия равна половине стороны, к которой она параллельна.
AMKN- параллелограмм, так как его противоположные стороны параллельны. Угол K = углу A = 45°, MH - высота этого параллелограмма. Угол AMH = 45°, значит треугольник AMH - прямоугольный равнобедренный. AM = 4 (половина AB).
По теореме Пифагора 4²=x²+x², отсюда x= √8, где x - высота MH и сторона AH.
BH1- высота треугольника ABC, равна 2MH = 2√8. Площадь треугольника равна (2√8*16)/2 = 16√8.
Сторона AC равна 16, а сторона AB=8, так как средняя линия равна половине стороны, к которой она параллельна.
AMKN- параллелограмм, так как его противоположные стороны параллельны. Угол K = углу A = 45°, MH - высота этого параллелограмма. Угол AMH = 45°, значит треугольник AMH - прямоугольный равнобедренный. AM = 4 (половина AB).
По теореме Пифагора 4²=x²+x², отсюда x= √8, где x - высота MH и сторона AH.
BH1- высота треугольника ABC, равна 2MH = 2√8. Площадь треугольника равна (2√8*16)/2 = 16√8.
Приложения:
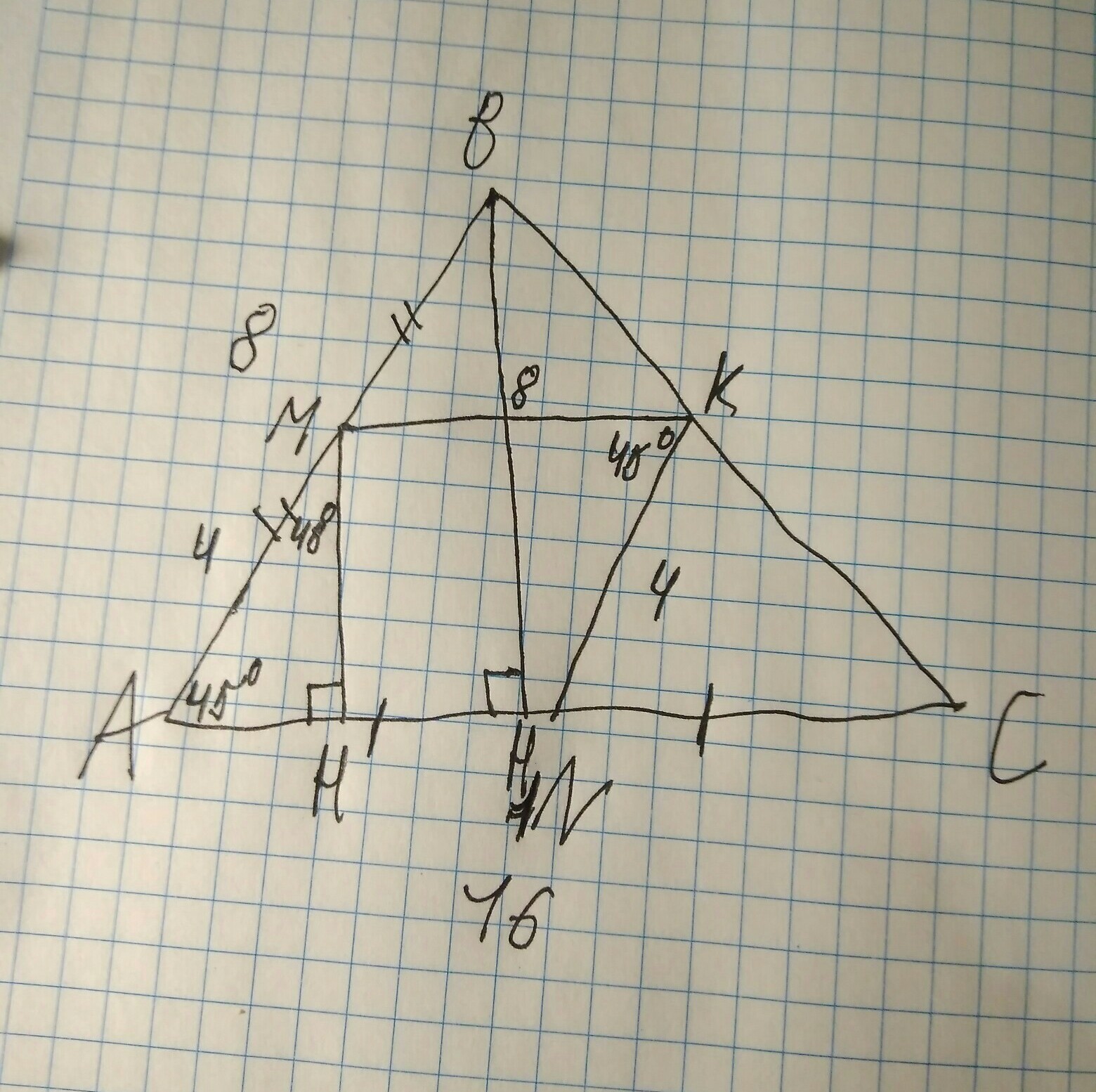
Новые вопросы
Химия,
1 год назад
Математика,
1 год назад
Математика,
7 лет назад
Биология,
7 лет назад
Математика,
8 лет назад