Сравнить arccos 1/6 и arcsin 1/5
Ответы на вопрос
Ответил Artem112
5
Сделаем обозначения:
![\arccos \frac{1}{6} =a; \ \arcsin \frac{1}{5} =b
\\\
\Rightarrow\cos a= \frac{1}{6} ; \ \sin b= \frac{1}{5}](https://tex.z-dn.net/?f=%5Carccos+%5Cfrac%7B1%7D%7B6%7D+%3Da%3B+%5C+%5Carcsin+%5Cfrac%7B1%7D%7B5%7D+%3Db%0A%5C%5C%5C%0A%5CRightarrow%5Ccos+a%3D+%5Cfrac%7B1%7D%7B6%7D+%3B+%5C+%5Csin+b%3D+%5Cfrac%7B1%7D%7B5%7D+ "\arccos \frac{1}{6} =a; \ \arcsin \frac{1}{5} =b
\\\
\Rightarrow\cos a= \frac{1}{6} ; \ \sin b= \frac{1}{5}")
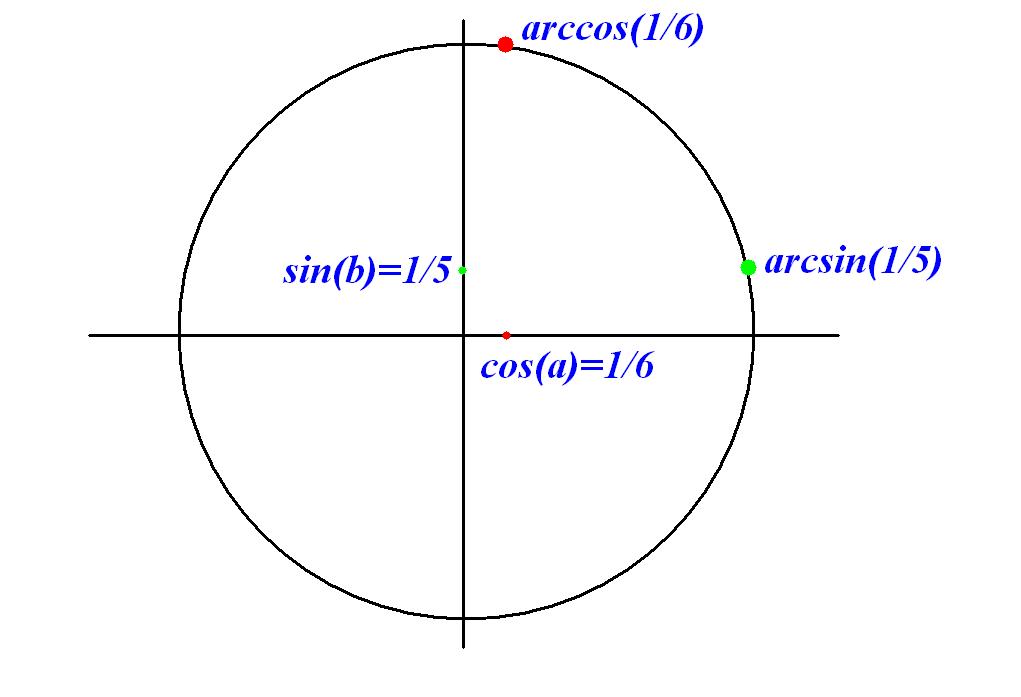
Если арксинус принимает отрицательные значения, то сам угол расположен в 4 четверти, если положительные - то в 1 четверти (наш случай)
Если арккосинус принимает отрицательные значения, то сам угол расположен в 2 четверти, если положительные - то в 1 четверти (наш случай)
Зная, что рассматриваемые углы лежат в 1 четверти используем основное тригонометрическое тождество:
![\cos b= \sqrt{1-\sin^2b} =\sqrt{1-( \frac{1}{5} )} = \frac{ \sqrt{24} }{5} = \frac{ 2\sqrt{6} }{5}
\\\
\Rightarrow \cos b>\cos a](https://tex.z-dn.net/?f=%5Ccos+b%3D+%5Csqrt%7B1-%5Csin%5E2b%7D+%3D%5Csqrt%7B1-%28+%5Cfrac%7B1%7D%7B5%7D+%29%7D+%3D+%5Cfrac%7B+%5Csqrt%7B24%7D+%7D%7B5%7D+%3D+%5Cfrac%7B+2%5Csqrt%7B6%7D+%7D%7B5%7D+%0A%5C%5C%5C%0A%5CRightarrow+%5Ccos+b%26gt%3B%5Ccos+a "\cos b= \sqrt{1-\sin^2b} =\sqrt{1-( \frac{1}{5} )} = \frac{ \sqrt{24} }{5} = \frac{ 2\sqrt{6} }{5}
\\\
\Rightarrow \cos b>\cos a")
В первой четверти при увеличении косинуса угла от 0 до 1 сам угол уменьшается от
до 0. Значит, b<a или 
Ответ:
Если арксинус принимает отрицательные значения, то сам угол расположен в 4 четверти, если положительные - то в 1 четверти (наш случай)
Если арккосинус принимает отрицательные значения, то сам угол расположен в 2 четверти, если положительные - то в 1 четверти (наш случай)
Зная, что рассматриваемые углы лежат в 1 четверти используем основное тригонометрическое тождество:
В первой четверти при увеличении косинуса угла от 0 до 1 сам угол уменьшается от
Ответ:
Приложения:
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
1 год назад
Алгебра,
7 лет назад
История,
7 лет назад