Спростіть вираз 3 и 4 ДАЮ 30 БАЛОВ!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
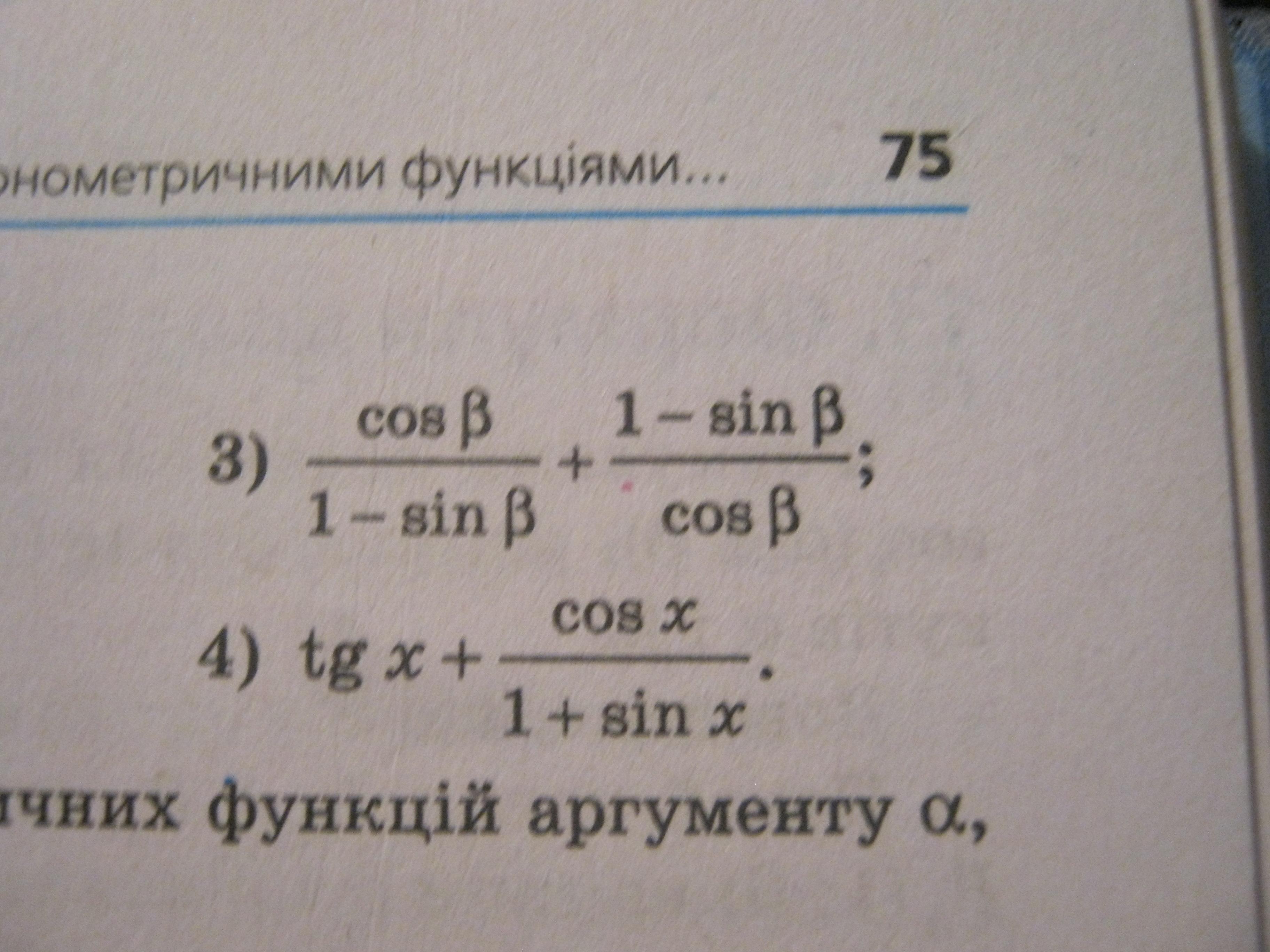
mawos:
photomath такое решает.
https://www.mathway.com/ru/Algebra
Ответы на вопрос
Ответил filuksistersp735lh
1
Ответ:
....
Пошаговое объяснение:
единственная формула:
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Литература,
2 года назад
География,
8 лет назад
Математика,
8 лет назад