спасите, пожалуйста... если несложно, то с рисунком ​

Ответ:

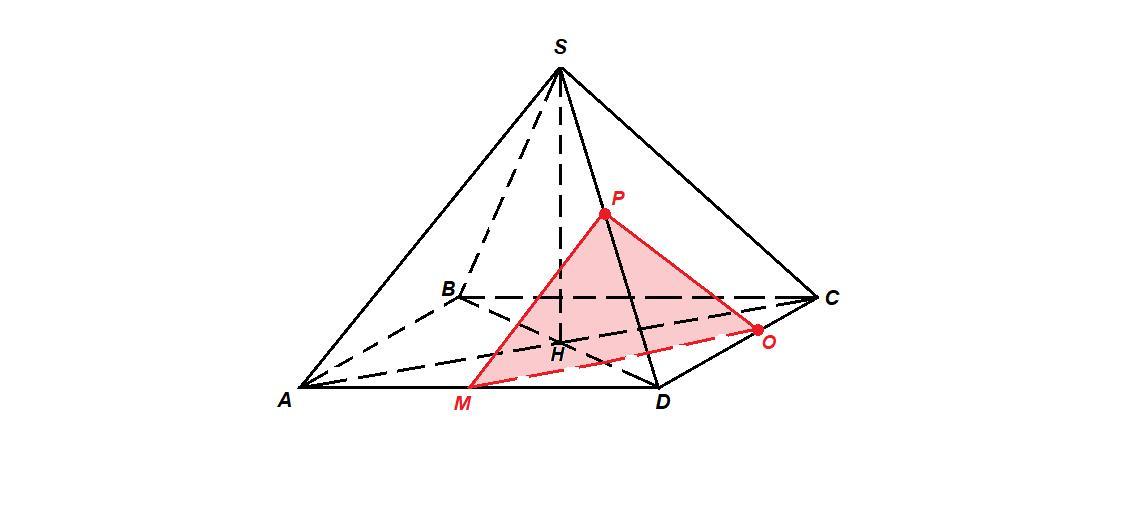
Проводим отрезок  РО, так как точки Р и О лежат в одной грани SDC.

В плоскости (АВС) через точку О проводим прямую ОМ║АС (М∈AD).

Соединяем точки Р и М.

РОМ - искомое сечение.

Докажем, что плоскость (РОМ) перпендикулярна плоскости (BSD).

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она так же перпендикулярна другой плоскости.

AC⊥BD как диагонали квадрата,

АС⊥SH, так как SH⊥(ABC), a AC⊂(ABC),    ⇒   AC⊥(BSD).

OM║AC,   ⇒   OM⊥(BSD).

А так как ОМ лежит в секущей плоскости, то

(РОМ)⊥(BSD).