спасайте, надо исследовать эту функцию. и объясните, пожалуйста, куда смещать/отображать график исходной функции при построении
Приложения:

Ответы на вопрос
Ответил spasibo3pajbrh
0
так как
то
функция чётная
функция определена для всех х
Dy:x€R
Еу:[0,+∞)
то есть функция ограничена , она принимает только неотрицательные значения (из-за свойств модуля)
и принимает вид:
каждый из этих промежутков
разбивается ещё на два (см фото)
при x≥0
x²+x-2≥0
(x-1)(x+2)≥0
[0,1)v[1;+∞)
при x<0
х²-х-2≥0
(х-2)(х+1)≥0
(-∞;-1]v(-1;0)
функция будет иметь следующий вид
на этих промежутках
у(х)=|f(x)|≥0, поэтому
решим у(х)=0
при х¹'²=±1 ( кстати, это нули функции), функция примет наименьшее значение =0
yнаибольшее =+∞
график на рисунке
Приложения:

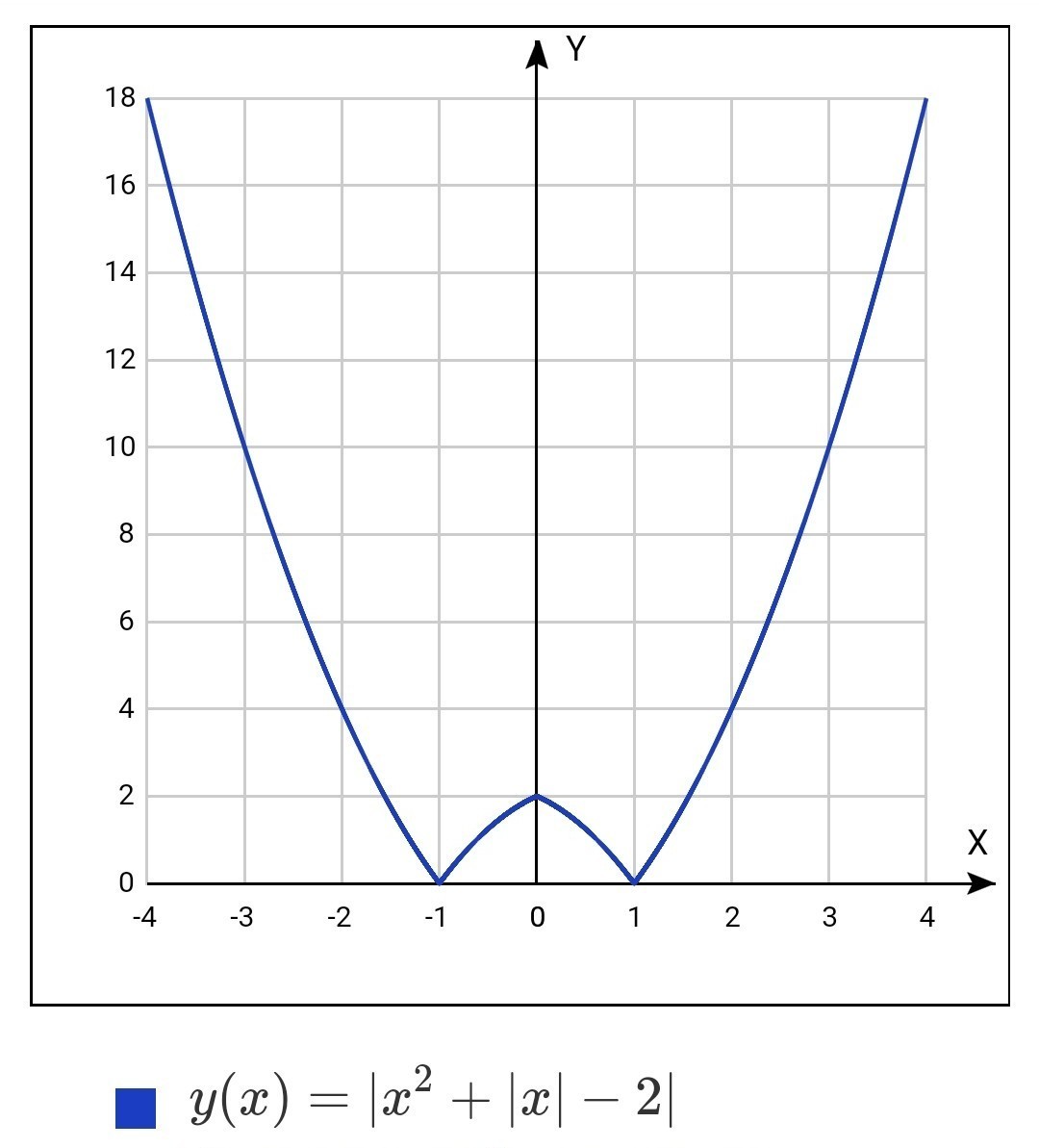
Новые вопросы