Составьте уравнения сторон треугольника, зная одну из его вершин А(3; -4) и уравнения двух высот: 7х-2у-1=0 и 2х-7у- 6=0. ( С чертежом)
dnepr1:
Как это понимать: А(3;B -4)? Может так: А(3; -4)?
наверное опечатка и А(3;-4)
все, верно, вы правы
опечатка произошла, исправила)
Ответы на вопрос
Ответил dnepr1
5
Стороны треугольника перпендикулярны высотам.
Используем свойство уравнения перпендикулярной прямой.
Для прямой Ах + Ву + С1 = 0 перпендикулярная прямая имеет такое уравнение: Вх - Ау+ С2 = 0.
Находим:
АВ: 7х + 2у + С = 0. Подставим координаты точки А.
7*3 + 2*(-4) + С = 0, отсюда С = 8 - 21 = -13.
Уравнение АВ: 7х + 2у - 13 = 0.
Аналогично для АС:
АС: 2х + 7у + С = 0. Подставляем координаты точки А.
2*3 + 7*(-4) + С = 0, отсюда С = 28 - 6 = 22.
Уравнение АС: 2х + 7у + 22 = 0.
Находим координаты точек В и С как точки пересечения прямых - стороны и высоты.
Получаем: В(1; 3) и С(-4; -2).
Уравнение ВС: х - у + 2 = 0.
Приложения:
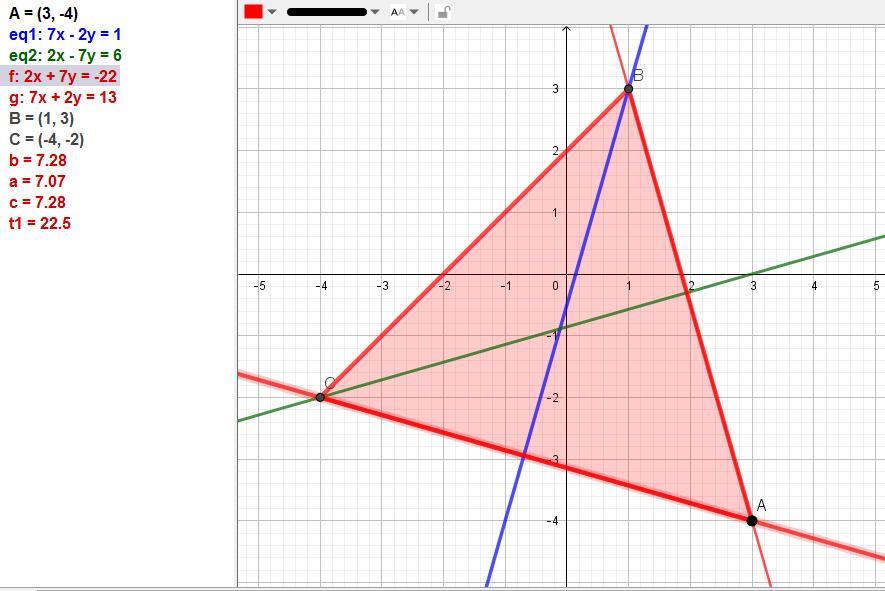
спасибо вам большое!!!
пожалуйста, если вас не затруднит, не могли бы вы мне помочь с ещё одной задачей на эту же тему, она у меня в вопросах
получается уравнение ВС мы можем найти только из рисунка?
Новые вопросы
Русский язык,
1 год назад
Математика,
2 года назад
Алгебра,
2 года назад
Физика,
8 лет назад
Алгебра,
8 лет назад