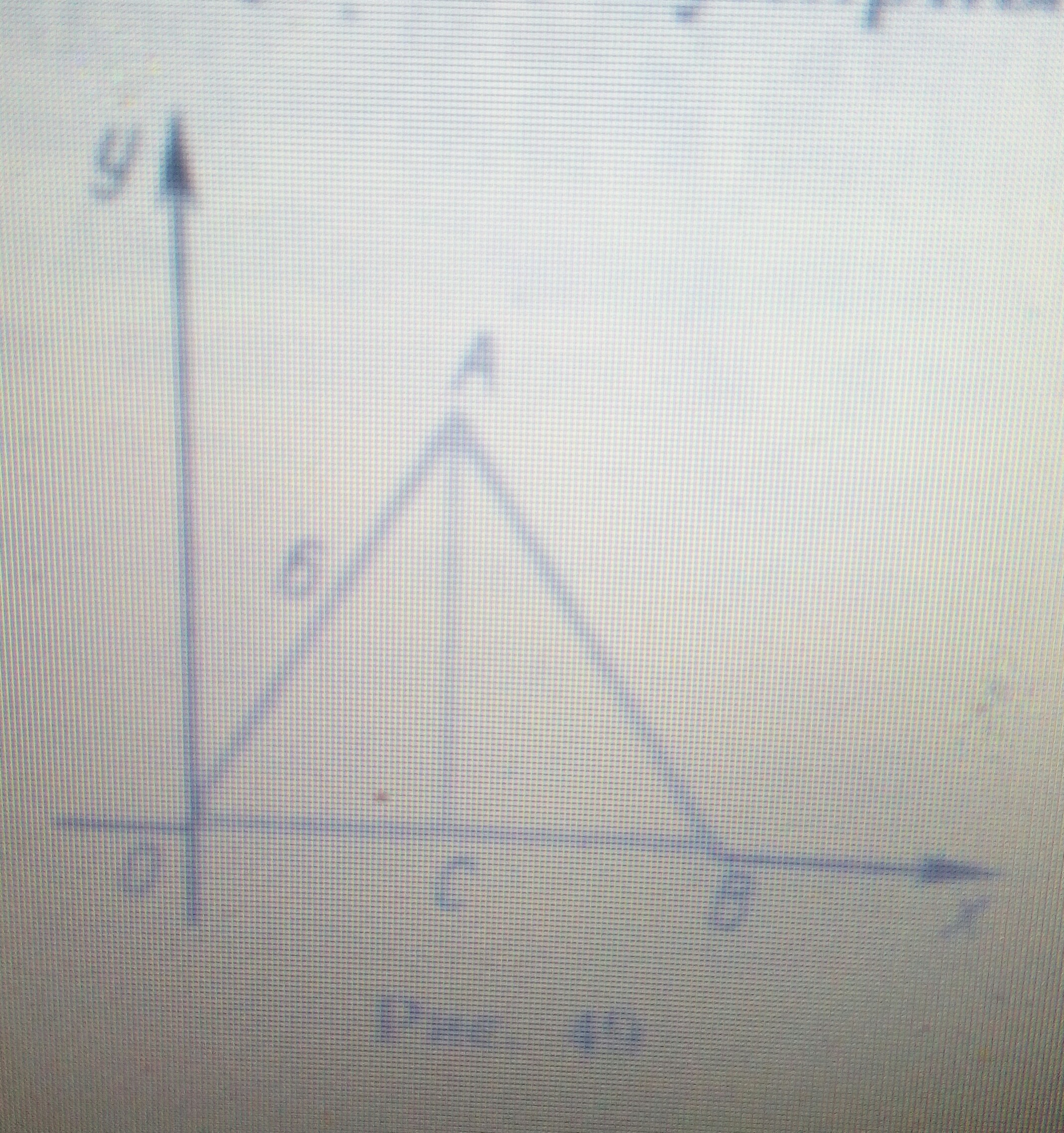
Составить уравнения строн AO и OB правильного треугольника AOB и его высоты AC (рис. 49)
Приложения:
Ответы на вопрос
Ответил DNHelper
0
Так как высота - ещё и медиана, а OB = 6, то OC = 3, т. е. x = 3. Отсюда для AC: x - 3 = 0
У правильного треугольника все углы по 60°. Коэффициент перед x равен тангенсу угла O - tg(60°) = √3. Так как прямая проходит через центр, свободный член равен нулю. Отсюда для OA: y = x√3 ⇒ -√3 * x + y = 0
OB лежит на Ox, поэтому для OB: y = 0
У правильного треугольника все углы по 60°. Коэффициент перед x равен тангенсу угла O - tg(60°) = √3. Так как прямая проходит через центр, свободный член равен нулю. Отсюда для OA: y = x√3 ⇒ -√3 * x + y = 0
OB лежит на Ox, поэтому для OB: y = 0
Новые вопросы