Составить уравнение касательной ( производная )
Приложения:
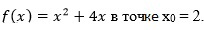
Ответы на вопрос
Ответил nKrynka
0
Решение
y = x² + 4x, x₀ = 2
Запишем уравнение касательной в общем виде:
y = y₀ + y'(x₀)(x - x₀)
По условию задачи x₀ = 2, тогда y₀ = 12
Теперь найдем производную:
y' = (x² + 4x)' = 2x + 4
следовательно:
f'(2) = 2*2 + 4 = 8
В результате имеем:
y = 12 + 8(x - 2)
y = 8x - 4
y = x² + 4x, x₀ = 2
Запишем уравнение касательной в общем виде:
y = y₀ + y'(x₀)(x - x₀)
По условию задачи x₀ = 2, тогда y₀ = 12
Теперь найдем производную:
y' = (x² + 4x)' = 2x + 4
следовательно:
f'(2) = 2*2 + 4 = 8
В результате имеем:
y = 12 + 8(x - 2)
y = 8x - 4
Ответил inkognitous
0
Спасибо
Ответил wangross
0
Дано:

Уравнение любой касательной в точке имеет вид:

Найдём всё, что можем для нашего уравнения.
1) Можно найти . Для этого просто подставим значение
. Для этого просто подставим значение  в уравнение функции:
в уравнение функции:

2) Дальше нам нужно найти производную функции в точке .
.
Сначала просто найдём производную нашей функции:

Теперь просто подставим в производную:
в производную:

Всё! Вуаля! Мы всё знаем для уравнения:

Итак, уравнение касательной:
 .
.
Уравнение любой касательной в точке имеет вид:
Найдём всё, что можем для нашего уравнения.
1) Можно найти
2) Дальше нам нужно найти производную функции в точке
Сначала просто найдём производную нашей функции:
Теперь просто подставим
Всё! Вуаля! Мы всё знаем для уравнения:
Итак, уравнение касательной:
Новые вопросы