сор по матем отдам все свои баллы​

( 1 )

5,6  ≤  a  ≤  5,8

2,1  ≤  b ≤  2,2

Периметр прямоугольника находится по формуле ⇒  P = 2 ( a + b ) , где  a - длинна прямоугольника, а b - ширина

Сначала возьмём за a и b самые маленькие значения, то есть 5,6 и 2,1

Теперь подставим самые большие значения, то есть 5,8 и 2,2

Получается неравенство  ⇒  15,4 ≤ P ≤ 16

( Что значит что периметр больше либо равен 15,4 , но меньше либо                     равен 16 )

Площадь прямоугольника находится по формуле ⇒  S = ab , где                 a - длинна прямоугольника, а b - ширина

Также подставим вместо a и b самые маленькие значения  5,6 и  2,1

Теперь наибольшие значения 5,8 и 2,2

Выходит неравенство  ⇒   11,76 ≤ S ≤ 12,76

( Что значит что площадь прямоугольника больше или равна 11,76 , но меньше либо равна 12,76 )

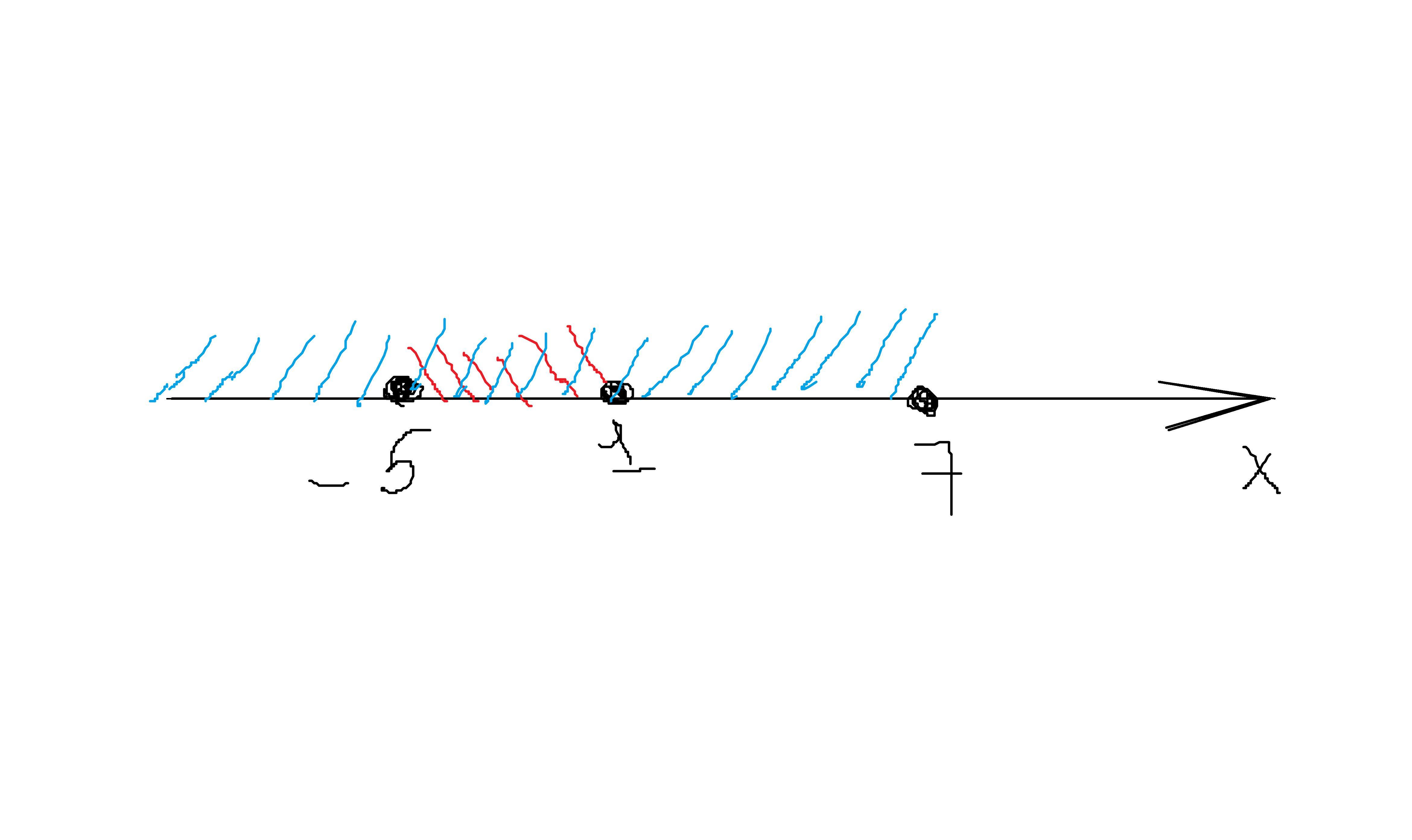
( 2 )

Пересечение: [ -5 ; 1 ]

Объединение: ( -∞ ; 7 ]

( фото ниже )

( 3 ) (а)                                  

-3 < x < 5

x ∈ ( -3 ; 5 )

(b)

-1,2 ≤ x < -1

x ∈ [-1,2 ; -1 )

( c )

-∞ < x < 5

x ∈ ( -∞ ; 5 )

( 4 )

x ∈ ( 5 ; 7 ]

Целыми решениями являются числа 6 и 7