Соотношение площадей вписанной и описанной окружностей =0.75. Периметр правильного многоугольника 12см. Сколько сторон имеет многоугольник и каковы радиусы окружностей.

чертеж в файле ниже кликай
1.
По условию S₁/S₂ = 0,75 => r²/R² = 0,75
r - радиус вписанной окружности
R  -  радиус описанной окружности
r² = 0,75R²
2.
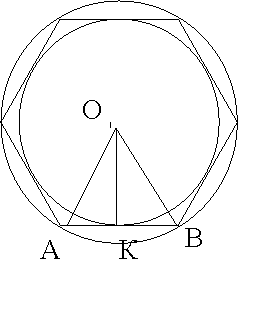
ΔАОВ  - один из секторных треугольников данного многоугольника
B ΔAOB  AO = BO = R 
OK ⊥AB  
OK = r 
В прямоугольном ΔAOK по теореме Пифагора   AK² = AO² - OK²
AK² = R² - r²
AK² = R² - 0,75R²
AK² = 0,25R²
√AK² = √(0,25R²)
AK = 0,5 R это значит, что катет АК равен половине гипотенузы АО, т.е R
Следовательно,  <AOK = 30°   => < AOB = 60°  ΔAOB - равносторонний
n = 360° : 60° = 6
n = 6 - это означает, что это шестиугольник
3.
P = 12 cм
a = 12 : 6 = 2 см - сторона
a = R = 2 cм 
r = √(0,75R²) = R/2√3 
r = 2/2 *√3 = √3 ≈ 1,7 cм
Ответ: шестиугольник n = 6; R = 2 cм r = √3  ≈1,7 cm