Алгебра, вопрос задал lavincester , 2 года назад

Сократите пример/Спростіть вираз

Приложения:

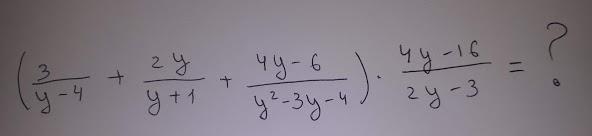
Ответы на вопрос

Ответил MatemaT123

Ответ:

$4$

Объяснение:

$\bigg (\dfrac{3}{y-4}+\dfrac{2y}{y+1}+\dfrac{4y-6}{y^{2}-3y-4} \bigg ) \cdot \dfrac{4y-16}{2y-3}=\bigg (\dfrac{3}{y-4}+\dfrac{2y}{y+1}+\dfrac{4y-6}{y^{2}-4y+y-4} \bigg ) \cdot$

$\cdot \dfrac{4y-16}{2y-3}=\bigg (\dfrac{3}{y-4}+\dfrac{2y}{y+1}+\dfrac{4y-6}{y(y-4)+1(y-4)} \bigg ) \cdot \dfrac{4y-16}{2y-3}=$

$= \bigg (\dfrac{3}{y-4}+\dfrac{2y}{y+1}+\dfrac{4y-6}{(y-4)(y+1)} \bigg ) \cdot \dfrac{4y-16}{2y-3}=\dfrac{3(y+1)+2y(y-4)+4y-6}{(y-4)(y+1)} \cdot$

$\cdot \dfrac{4(y-4)}{2y-3}=\dfrac{3y+3+2y^{2}-8y+4y-6}{(y-4)(y+1)} \cdot \dfrac{4(y-4)}{2y-3}=\dfrac{2y^{2}-y-3}{(y-4)(y+1)} \cdot \dfrac{4(y-4)}{2y-3}=$

$=\dfrac{4(2y^{2}-y-3)(y-4)}{(y-4)(y+1)(2y-3)}=\dfrac{4(2y^{2}-y-3)}{2y^{2}-3y+2y-3}=\dfrac{4(2y^{2}-y-3)}{2y^{2}-y-3}=4;$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

1) В цвету трава-косить пора. 2) Красная девица сидит в темнице, а коса на улице. 3) Коли лед-доставай серебро, возьмешь серебро-бери золото. 4) Если лень прикоснется, то лентяй за работу не...

Русский язык, 1 год назад

СРОЧНО ПОМОГИТЕ!!!Однако они становятся путешественниками, несмотря на трудности, которые им приходится преодолевать в пути.- синтаксический разбор...

Литература, 2 года назад

Разберите следующие предложения по членам. Солнце светило уже не по-весеннему, а по-летнему. Старик уверенно, ловко, по-молодому работал вёсла- ми. Валёк по-прежнему лежал на траве и задумчиво...

Математика, 2 года назад

какую сумму следует положить на сбережение в банк, выплачивающего 8% годовых,чтобы по истечении года получить 162 тыс.тенге? помогите пж...

Литература, 8 лет назад

Гадкий утёнок ..разделить на 5 частей и придумать пасловицу к сказке и озоглавить все 5 предложений...

Математика, 8 лет назад

Вычислите: i^27+i^33 (не надо писать "60" ибо кину жалобу)...