Алгебра, вопрос задал MAP12 , 1 год назад

Снова не идет матан , кто может помочь решить. будут очень благодарен) 11 кл

Приложения:

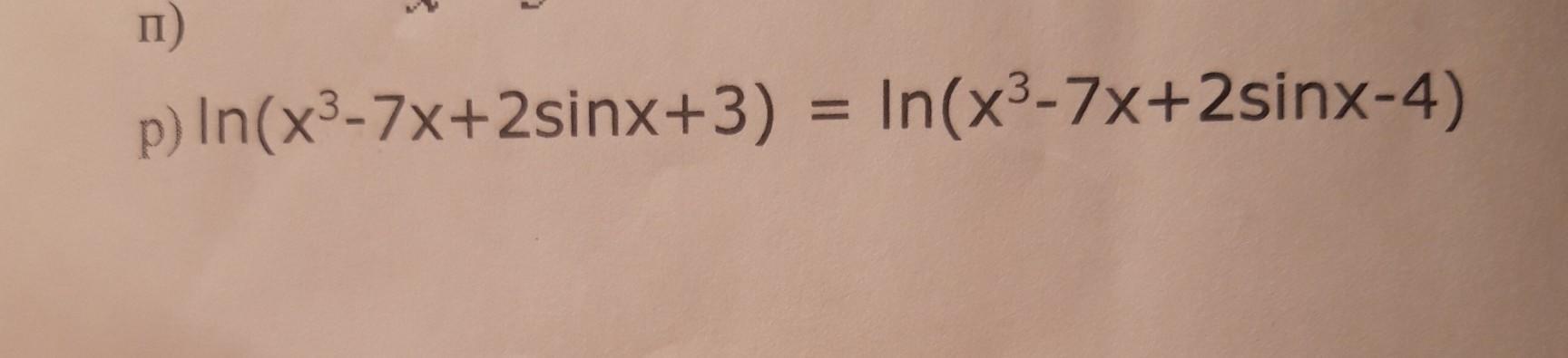
Ответы на вопрос

Ответил Удачник66

Ответ:

Нет решений

Объяснение:

Если два логарифм с одинаковым основанием равны, то равны и выражения под логарифмом.

x^3 - 7x + 2sin x + 3 = x^3 - 7x + 2sin x - 4

Сокращаем одинаковые элементы

3 = - 4

Этого не может быть, значит, решений нет.

Ответил Olga8128

Ответ: нет решений.

Объяснение:

Если есть два равных логарифма с одинаковым основанием (так как логарифмы натуральные, то основание - число e), то равны и выражения под логарифмом.

То есть:

$In (x^3-7x+2sin (x)+3)=In(x^3-7x+2sin(x)-4)\\\\\Rightarrow x^3-7x+2sin (x)+3 =x^3-7x+2sin(x)-4\\$

Теперь сокращаем одинаковые части ( $x^3-7x+2sin(x)$ ) и получаем:

$3 = -4$

Но это, естесственно, неправда, поэтому решений у уравнения нет.

antonovm: как вы лихо логарифмы выкидывайте ( это относится и к предыдущему решению ) ; ln( 1-x) = ln(x-1) ; 1-x = x-1 ; x = 1 ? (вот так делать нельзя) , ну нет решений , а если бы были ? переход к следствию неравносилен , должна быть система

Удачник66: Так как логарифмы одинаковые - натуральные, то их можно одновременно отбросить. Ваш пример ln(1-x) = ln(x-1) не подходит, потому что под логарифмом должно быть положительное число, а два противоположных не могут быть оба положительными. При x = 1 будет x-1 = 1-x = 0, а логарифм нуля не определен.

antonovm: правильно, под логарифмом должно быть положительное число , поэтому уравнение ln( f(x)) = ln(g(x) ) равносильно системе : f(x) = g(x) и f(x) > 0 или f(x) = g(x) и g(x)>0 , просто отбрасывать логарифмы нельзя , иначе может получится посторонние корни , в этом примере просто повезло , что корней нет , но ваш переход неправилен

antonovm: так же нельзя просто выбросить корни в уравнении : корень из(f(x)) = корень из(g(x)) , равенство корней не равносильно равенству подкоренных выражений

antonovm: и почему мой пример не подходит ? , я решал как вы : просто выбросил логарифмы и стал решать полученное уравнение , но полученное уравнение в отличии от вашего примера просто имеет корень , а ваше корней не имеет

antonovm: скорее всего в условии этого примера где-то ошибка , уж слишком он примитивен

antonovm: " Если два логарифм с одинаковым основанием равны, то равны и выражения под логарифмом." - вот это неверно , надо добавить : при условии , что оба они положительны

antonovm: ну или в конце решения сделать проверку , но здесь просто проверять нечего ( повезло)

Удачник66: Насчёт условия, что выражения под логарифмом должны быть оба положительные - это само собой разумеется, от отрицательного числа нельзя взять логарифм.

Удачник66: А насчёт ошибки в задании я полностью согласен, слишком просто все получается.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

срочноооо!!!!!!! дам 90 балов...

География, 1 год назад

Як потрібно одягнутися при сходженні на г. Говерлу, якщо температура повітря біля її підніжжя +15 0С. Якою буде температура на вершині? При розрахунках пам'ятайте про відмінність відносної і...

Геометрия, 1 год назад

один из катетов прямоугольного треугольника равен 10 см а высота опущенная к гипотенузе равна 6 см Найдите его второй катет...

Физика, 1 год назад

Штучний супутник обертається навколо Землі по круговій орбіті радіусом R з періодом обертання 2 доби. Вкажіть 1 – шлях і 2 – модуль переміщення супутника за 0,25 доби...

Математика, 6 лет назад

Найдите число 15% которого равны 60...

Геометрия, 6 лет назад

Сколько существует неравных друг другу треугольников с периметром, равным 7, если длины сторон этих треугольников выражаются целыми числами? Помогите срочно!!!!!!