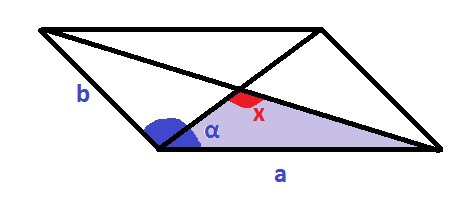
Смежные стороны параллелограмма равны а и b, a один из его углов равен α. Найдите угол между диагоналями параллелограмма.
Ответы на вопрос
Ответил Artem112
0
Если одни угол параллелограмма равен α, то противолежащий ему тоже равен α, а два других равны (180-α).
По теореме косинусов находим диагонали:
![d_1^2=a^2+b^2-2abcos alpha
\
d_2^2=a^2+b^2-2abcos (180-alpha )=a^2+b^2+2abcos alpha](https://tex.z-dn.net/?f=d_1%5E2%3Da%5E2%2Bb%5E2-2abcos+alpha+%0A%5C%0Ad_2%5E2%3Da%5E2%2Bb%5E2-2abcos+%28180-alpha+%29%3Da%5E2%2Bb%5E2%2B2abcos+alpha+ "d_1^2=a^2+b^2-2abcos alpha
\
d_2^2=a^2+b^2-2abcos (180-alpha )=a^2+b^2+2abcos alpha")
Диагонали параллелограмма точкой пересечения делятся пополам. Рассмотрим треугольник со сторонами d₁/2; d₂/2; a. Теорема косинусов для этого треугольника:
![a^2=( frac{d_1}{2})^ 2+( frac{d_2}{2})^ 2-2cdot frac{d_1}{2}cdot frac{d_2}{2}cos x
\
a^2=frac{1}{4}(d_1^2+d_2^2)- frac{1}{2}d_1d_2cos x
\
a^2=frac{1}{4}(a^2+b^2-2abcos alpha +a^2+b^2+2abcos alpha )-
\
-frac{cos x}{2} sqrt{(a^2+b^2-2abcos alpha)(a^2+b^2+2abcos alpha)}
\
a^2=frac{1}{4}(2a^2+2b^2 )-frac{cos x}{2} sqrt{(a^2+b^2)^2-(2abcos alpha)^2}
\
a^2=frac{1}{2}(a^2+b^2 )-frac{cos x}{2} sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha}](https://tex.z-dn.net/?f=a%5E2%3D%28+frac%7Bd_1%7D%7B2%7D%29%5E+2%2B%28+frac%7Bd_2%7D%7B2%7D%29%5E+2-2cdot+frac%7Bd_1%7D%7B2%7Dcdot++frac%7Bd_2%7D%7B2%7Dcos+x%0A%5C%0Aa%5E2%3Dfrac%7B1%7D%7B4%7D%28d_1%5E2%2Bd_2%5E2%29-+frac%7B1%7D%7B2%7Dd_1d_2cos+x%0A%5C%0Aa%5E2%3Dfrac%7B1%7D%7B4%7D%28a%5E2%2Bb%5E2-2abcos+alpha+%2Ba%5E2%2Bb%5E2%2B2abcos+alpha+%29-+%0A%5C%0A++-frac%7Bcos+x%7D%7B2%7D+sqrt%7B%28a%5E2%2Bb%5E2-2abcos+alpha%29%28a%5E2%2Bb%5E2%2B2abcos+alpha%29%7D+%0A%5C%0Aa%5E2%3Dfrac%7B1%7D%7B4%7D%282a%5E2%2B2b%5E2+%29-frac%7Bcos+x%7D%7B2%7D+sqrt%7B%28a%5E2%2Bb%5E2%29%5E2-%282abcos+alpha%29%5E2%7D+%0A%5C%0Aa%5E2%3Dfrac%7B1%7D%7B2%7D%28a%5E2%2Bb%5E2+%29-frac%7Bcos+x%7D%7B2%7D+sqrt%7B%28a%5E2%2Bb%5E2%29%5E2-4a%5E2b%5E2cos%5E2+alpha%7D+ "a^2=( frac{d_1}{2})^ 2+( frac{d_2}{2})^ 2-2cdot frac{d_1}{2}cdot frac{d_2}{2}cos x
\
a^2=frac{1}{4}(d_1^2+d_2^2)- frac{1}{2}d_1d_2cos x
\
a^2=frac{1}{4}(a^2+b^2-2abcos alpha +a^2+b^2+2abcos alpha )-
\
-frac{cos x}{2} sqrt{(a^2+b^2-2abcos alpha)(a^2+b^2+2abcos alpha)}
\
a^2=frac{1}{4}(2a^2+2b^2 )-frac{cos x}{2} sqrt{(a^2+b^2)^2-(2abcos alpha)^2}
\
a^2=frac{1}{2}(a^2+b^2 )-frac{cos x}{2} sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha}")
![2a^2=a^2+b^2-cos x sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha}
\
b^2-a^2=cos x sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha}
\
cos x= frac{b^2-a^2}{ sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha} }
\
Rightarrow x=arccos frac{b^2-a^2}{ sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha} }](https://tex.z-dn.net/?f=2a%5E2%3Da%5E2%2Bb%5E2-cos+x+sqrt%7B%28a%5E2%2Bb%5E2%29%5E2-4a%5E2b%5E2cos%5E2+alpha%7D+%0A%5C%0Ab%5E2-a%5E2%3Dcos+x+sqrt%7B%28a%5E2%2Bb%5E2%29%5E2-4a%5E2b%5E2cos%5E2+alpha%7D+%0A%5C%0Acos+x%3D+frac%7Bb%5E2-a%5E2%7D%7B+sqrt%7B%28a%5E2%2Bb%5E2%29%5E2-4a%5E2b%5E2cos%5E2+alpha%7D+%7D+%0A%5C%0ARightarrow+x%3Darccos+frac%7Bb%5E2-a%5E2%7D%7B+sqrt%7B%28a%5E2%2Bb%5E2%29%5E2-4a%5E2b%5E2cos%5E2+alpha%7D+%7D+ "2a^2=a^2+b^2-cos x sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha}
\
b^2-a^2=cos x sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha}
\
cos x= frac{b^2-a^2}{ sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha} }
\
Rightarrow x=arccos frac{b^2-a^2}{ sqrt{(a^2+b^2)^2-4a^2b^2cos^2 alpha} }")
По теореме косинусов находим диагонали:
Диагонали параллелограмма точкой пересечения делятся пополам. Рассмотрим треугольник со сторонами d₁/2; d₂/2; a. Теорема косинусов для этого треугольника:
Приложения:
Новые вопросы
Английский язык,
2 года назад
Английский язык,
2 года назад
Музыка,
9 лет назад
Биология,
9 лет назад
Обществознание,
9 лет назад