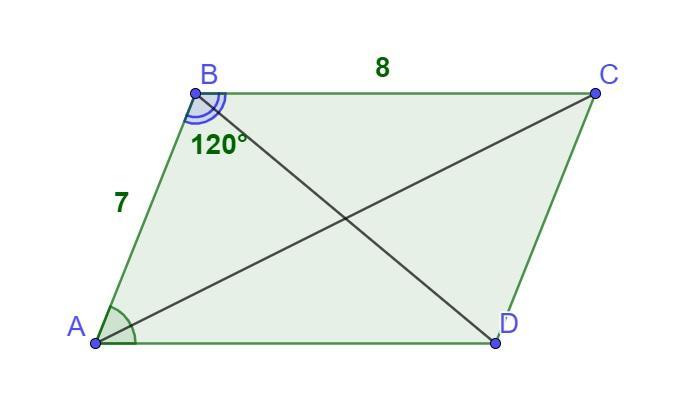
смежные стороны параллелограмма равны 7 см и 8 см а угол между ними равен 120° найдите диагонали параллелограмма и его площадь. пожалуйста, срочно надо​

Ответ:

Длины диагоналей параллелограмма равны 13 см и √57 см, а его площадь 28√3 см²

Пошаговое объяснение:

Смежные стороны параллелограмма равны 7 см и 8 см, а угол между ними равен 120°. Найдите диагонали параллелограмма и его площадь.

Пусть ABCD - данный параллелограмм, АВ = 7 см, ВС = 8 см, ∠В = 120°.

Найдём его диагонали AC и BD и его площадь S.

1.

По теореме косинусов найдём диагональ АС.

АС² = АВ² + ВС² - 2 · АВ · ВС · cos∠B

Подставим значения и рассчитаем:

AC² = 7² + 8² - 2 · 7 · 8 · cos 120°

cos 120° = cos (180° - 60°) = - cos 60° = -1/2

Тогда:

АС² = 49 + 64 -2 · 56 · (-1/2) = 169

АС = √169 = 13 (см)

2.

Так как углы, прилежащие к одной стороне параллелограмма, в сумме дают 180°, то:

∠А = 180° - ∠В = 180° - 120° = 60°

Тогда вторая диагональ (по теореме косинусов) будет равна:

BD² = AB² + AD² - 2 · AB · AD · cos ∠A

AD = BC = 8 (см) - как противоположные стороны параллелограмма.

Тогда:

BD² = 7² + 8² - 2 · 7 · 8 · cos 60° = 49 + 64 - 2 · 56 · 1/2 = 57

BD = √57 (см)

3.

Площадь параллелограмма можно найти по формуле:

S(ABCD) = AB · BC · sin ∠ B

S(ABCD) = 7 · 8 · sin 60° = 56 · (√3/2) = 28√3 см²

#SPJ1