Алгебра, вопрос задал Barbi54 , 6 лет назад

СКОРО ЗДАВАТИ На колі позначено точки A,B i C так, що AB=9 см, BC=40 см, AC=41 см. Знайдіть радіус кола.

Приложения:

Ответы на вопрос

Ответил NNNLLL54

Ответ: R=20,5 см .

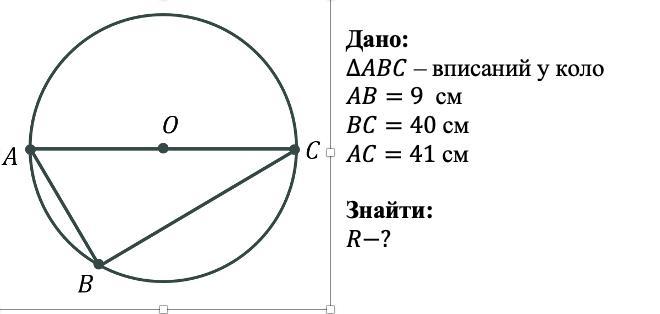
ΔАВС , АВ=9 см , ВС=40 см , АС=41 см .

Так как АС - диаметр (видно из рисунка) , то радиус R=41:2=20,5 (см) .

Проверим это . ΔАВС - прямоугольный, так как вписанный угол АВС опирающийся на диаметр, равен 90° . Тогда должна выполняться теорема Пифагора: АС²=АВ²+ВС² ,

АВ²+ВС²=81+1600=1681=41² ⇒ действительно ΔАВС прямоугольный треугольник . Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы : R=20,5 cм .

Ответил Аноним

найдем по Герону площадь S треугольника АВС со сторонами

а=9см ;b=40см;с=41см:

1)полупериметр (9+40+41)/2=45/см/

р-а=45-9=36/см/

р-b=45-40=5/см/

р-с=45-41=4/см/

2) S=√(45*36*5*4)=√(5*9*36*5*4)=5*3*6*2=180/см²/

3) R=а*b*с/(4S)=9*40*41/(4*180)=20.5/см/

Ответ 20.5 см

Предыдущий вопрос

Следующий вопрос