сколько решений имеет система уравнений х2+y2=а ,xy=1 при различных параметрах а?
Ответы на вопрос
Ответил NeZeRAvix
0
Начнем с того, что выражение x²+y²≥0 при любых x и y, значит отрицательные значения a мы не рассматриваем.
Первое уравнение системы:
x²+y²=a
это уравнение окружности с центром в начале координат. Значение a задает радиус окружности.
Второе уравнение системы:
xy=1
это гипербола y=1/x, лежащая в 1 и 3 координатных четвертях. Самые близкие к началу координат точки, принадлежащие этому графику - (1;1)
и (-1;-1)
Рассмотрим три случая:
1)
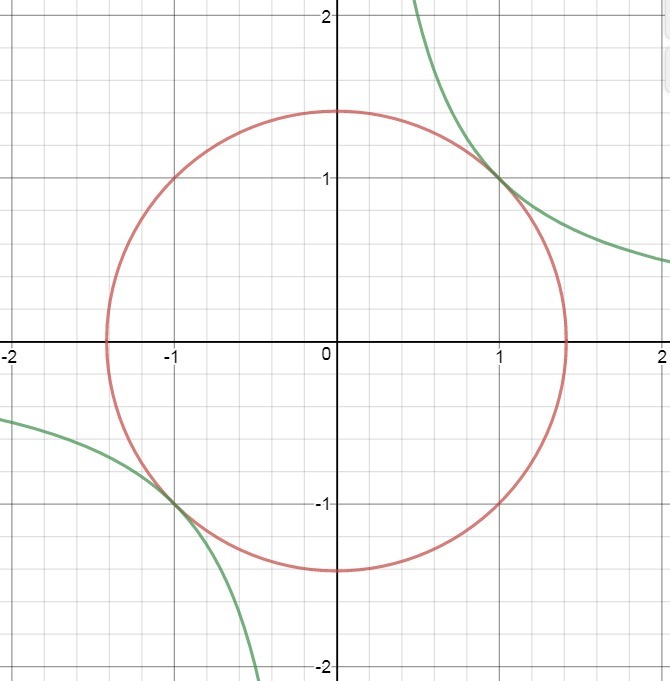
a таково, что окружность проходит через точки (-1;-1) и (1;1), следовательно система имеет 2 решения. Найдем a.
По теореме Пифагора из прямоугольного треугольника с катетами равными 1, гипотенуза=радиус=√(1²+1²)=√2 ⇒ a=√2²=2
При a=2 система имеет 2 решения
2)
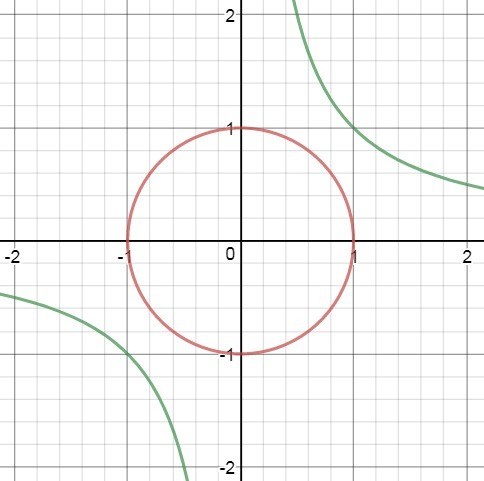
а таково, что окружность не пересекает гиперболу y=1/x. это произойдет в том случае, если радиус меньше двух.
При a∈[0;2) система не имеет решений
3)
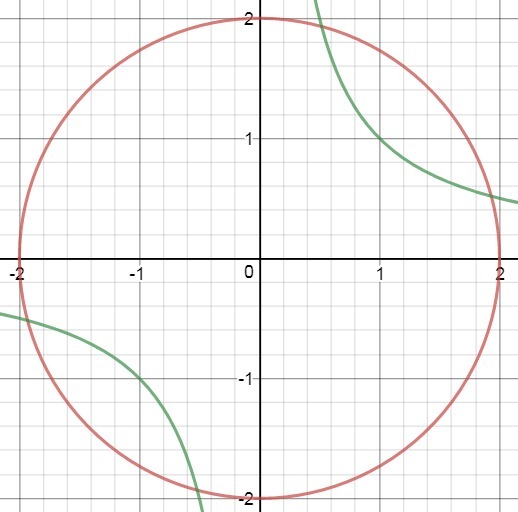
а таково, что окружность пересекает гиперболу в 4 точках. это произойдет, если радиус больше двух.
При a∈(2;+∞) система имеет 4 решения
Графики для каждого случая приложены для наглядности.
Первое уравнение системы:
x²+y²=a
это уравнение окружности с центром в начале координат. Значение a задает радиус окружности.
Второе уравнение системы:
xy=1
это гипербола y=1/x, лежащая в 1 и 3 координатных четвертях. Самые близкие к началу координат точки, принадлежащие этому графику - (1;1)
и (-1;-1)
Рассмотрим три случая:
1)
a таково, что окружность проходит через точки (-1;-1) и (1;1), следовательно система имеет 2 решения. Найдем a.
По теореме Пифагора из прямоугольного треугольника с катетами равными 1, гипотенуза=радиус=√(1²+1²)=√2 ⇒ a=√2²=2
При a=2 система имеет 2 решения
2)
а таково, что окружность не пересекает гиперболу y=1/x. это произойдет в том случае, если радиус меньше двух.
При a∈[0;2) система не имеет решений
3)
а таково, что окружность пересекает гиперболу в 4 точках. это произойдет, если радиус больше двух.
При a∈(2;+∞) система имеет 4 решения
Графики для каждого случая приложены для наглядности.
Приложения:
Ответил shakajaaaas
0
большое спасибо)
Новые вопросы
Геометрия,
2 года назад
Физика,
2 года назад
История,
7 лет назад
Обществознание,
7 лет назад
Математика,
9 лет назад