Скласти рівняння кола, яке проходить через точки М(-3;7), В(- 8;2),К(- 6;- 2)
Ответы на вопрос
Ответ: (x+3)²+(y-2)²=25
Объяснение:
Уравнение окружности в общем виде:
(x-Xo)²+(y-Yo)²=R²
Xo;Yo - координаты центра окружности
R -радиус окружности
Подставив координаты известных трех точек , получим систему уравнений с 3-мя неизвестными:
1. (-3-Xo)²+(7-Yo)²=R²
2. (-8-Xo)²+(2-Yo)²=R²
3. (-6-Xo)²+(-2-Yo)²=R²
Вычтем из (2) (3)
=> 64+16Xo+Xo² +4-4Yo+Yo²-36-12Xo-Xo²-4-4Yo-Yo²=0
28+4Xo-8Yo=0=> 7+Xo-2Yo=0 (4)
Вычтем из (2) (1)
=> 64+16Xo+Xo² +4-4Yo+Yo²-9-6Xo-Xo²-49+14Yo-Yo²=0
10+10Xo+10Yo=0=> 1+Xo+Yo=0 (5)
-Получили систему из 2-х уравнений (4) и (5) с 2-мя неизвестными.
Вычтем из (4) (5) получим
6-3Yo=0 => Yo=2
Подставим Yo=2 в (5)
1+Xo+2=0
Xo=-3
Подставим Yo=2 и Xo=-3 в (1). Получим:
(-3-(-3))²+(7-2)²=R² => 0+5²=25=R²
Тогда уравнение окружности :
(x+3)²+(y-2)²=25
Ответ: (x+3)² + (y-2)² =25.
Объяснение:
Составить уравнение круга, проходящего через точки
М(-3;7),
В(- 8;2),
К(- 6;- 2).
Уравнение окружности имеет вид
(x-x0)² + (y-y0)² = R², где x0 и y0 - координаты центра окружности.
радиусы R окружности OM, OB и OK - равны между собой
ОМ² =(xM-xO)² + (yM-yO) = (-3-x0)² + (7-y0)²;
OB² = (-8-x0)² + (2-y0)²;
OK²=(-6-x0)²+ (-2-y0).
OM² = OB² => (-3-x)² + (7-y)² = (-8-x)² + (2-y)².
Раскрываем скобки и приводим подобные слагаемые. Получаем выражение
x²+6x+y²-14y+58 = x²+16x+y²-4y+68;
x= -y-1.
---------
OB² = OK² => (-8-x)² + (2-y)² = (-6-x)²+ (-2-y)².
Раскрываем скобки и приводим подобные слагаемые. Получаем выражение
x²+16x+y²-4y+68 = x²+12x+y²+4y+40;
x= 2y-7,
-------------------
-y-1 = 2y-7;
y0=2.
x= 2*2-7,
x0=-3.
---------------------
Центр окружности О(-3;2).
-------------
Радиус окружности R² = OM² = (-3-x0)² + (7-y0)² = (-3-(-3))² + (7-2)² =
=0² + 5² =25.
Уравнение окружности имеет вид
(x+3)² + (y-2)² =25.
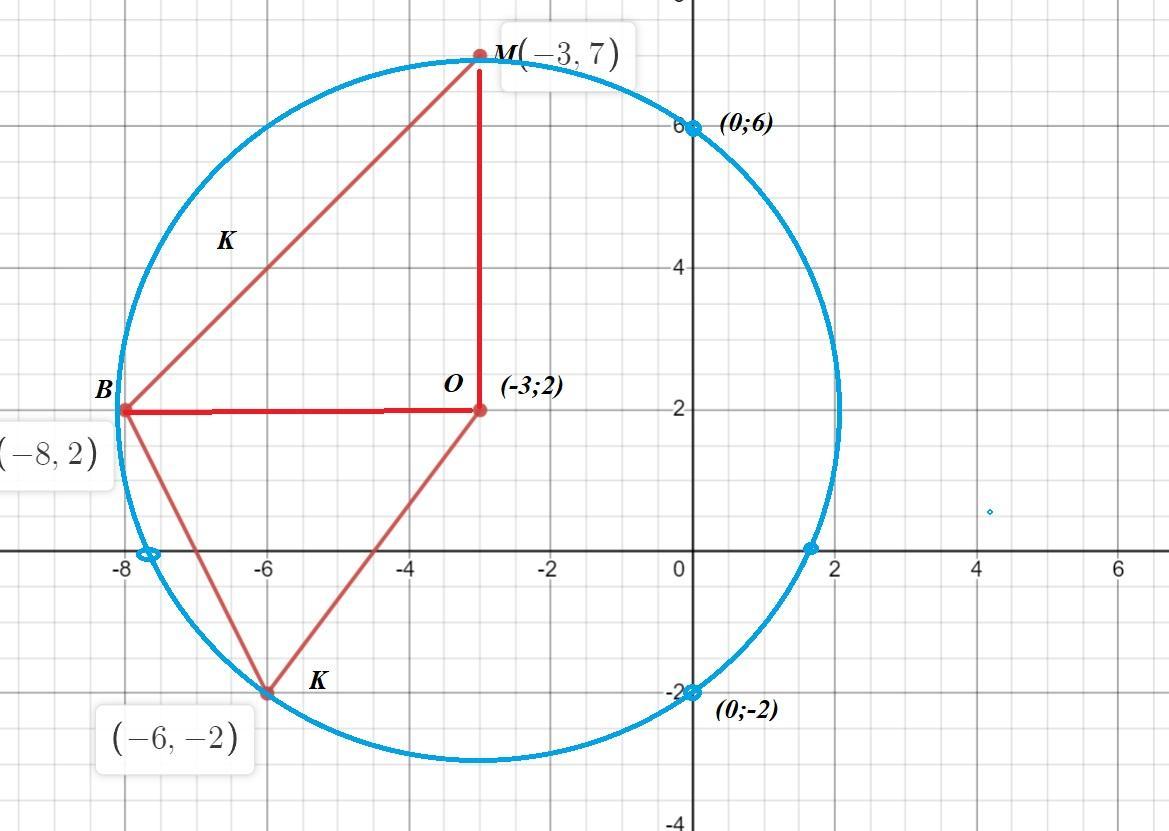
liftec74, есть ещё один способ ( без систем ) : центр - точка пересечения серединных перпендикуляров к сторонам , а радиус - расстояние от центра до любой вершины