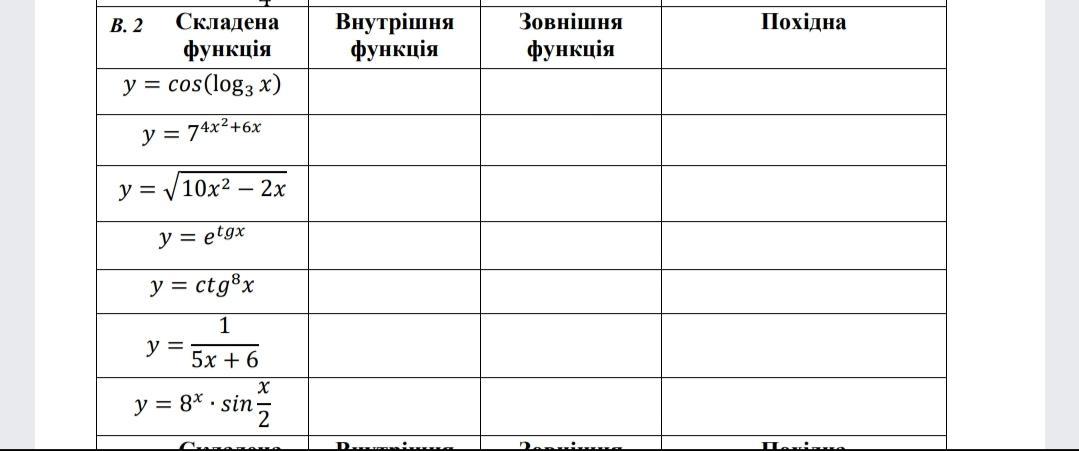
Математика, вопрос задал svalve484 , 2 года назад

Складена функція, найти

Приложения:

Ответы на вопрос

Ответил DimaPuchkov

1. Внутренняя: $t= \log_3x$

Внешняя: $\cos{t}$

Производная:

$y'=(\cos{(\log_3x}))'=-\sin{(\log_3x)}\cdot (\log_3x)'=-\sin{(\log_3x)}\cdot\frac{1}{x\cdot \ln{3}}$

Внутренняя: $t=4x^2+6x$

Внешняя: $7^t$

Производная:

$y'=(7^{4x^2+6x})'=7^{4x^2+6x}\cdot \ln{7}\cdot (4x^2+6x)'=7^{2x\cdot(2x+3)}\cdot (8x+6)\cdot \ln{7}$

Внутренняя: $t=10x^2-2x$

Внешняя: $\sqrt{t}$

Производная:

$y'=(\sqrt{10x^2-2x})'=((10x^2-2x)^\frac{1}{2})'=\frac{1}{2}\cdot (10x^2-2x)^{-\frac{1}{2}}\cdot (10x^2-2x)'= \\ \\ = \frac{1}{2\cdot \sqrt{10x^2-2x}}\cdot (20x-2)=\frac{ 10x-1}{\sqrt{10x^2-2x}}=\frac{ 10x-1}{\sqrt{2x\cdot (5x-1)}}$

Внутренняя: $t = tg \, x$

Внешняя: $e^t$

Производная:

$y'=(e^{tg \, x})'=e^{tg \, x}\cdot (tg \, x)'=e^{tg \, x}\cdot \frac{1}{\cos^2{x}}$

Внутренняя: $t =ctg \, x$

Внешняя: $t^8$

Производная:

$y'=(ctg^8 \, x)'=8\, ctg^7 \, x \cdot (ctg \, x)'=8\, ctg^7 \, x \cdot (-\frac{1}{\sin^2{x}})=-\frac{8\, ctg^7 \, x}{\sin^2{x}}$

(или можно еще упростить: $-\frac{8\, ctg^7 \, x}{\sin^2{x}}=-\frac{8\cos^7{x}}{\sin^9{x}}$ )

Внутренняя: $t =5x+6$

Внешняя: $t^{-1}$

Производная:

$y'=(\frac{1}{5x+6})'=((5x+6)^{-1})'=-(5x+6)^{-2}\cdot (5x+6)' =-\frac{5}{(5x+6)^2}$

Внутренняя: $t=x; \ \ r=\frac{x}{2}$

Внешняя: $8^t; \ \ \ \sin{r}$

Производная:

$(uv)'=u'\cdot v+u\cdot v' \\ \\ y' =(8^x\cdot \sin{\frac{x}{2}})'=(8^x)'\cdot \sin{\frac{x}{2}}+8^x\cdot (\sin{\frac{x}{2}})'=8^x\cdot \ln{8}\cdot \sin{\frac{x}{2}}+8^x\cdot \cos{\frac{x}{2}}\cdot (\frac{x}{2})'=\\ \\ = 8^x\cdot (\ln{8}\cdot \sin{\frac{x}{2}}+\frac{1}{2}\cos{\frac{x}{2}})=2^{3x}\cdot (\ln{8}\cdot \sin{\frac{x}{2}}+\frac{1}{2}\cos{\frac{x}{2}})$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

продолжи цепочки слов сирень липа...

Английский язык, 1 год назад

помогите пожалуйста. срочно...

Математика, 2 года назад

a) 190,62: : (8,127: (4,5x + 2,11)) = 70,6; С проверкой пожалуйста...

Українська мова, 2 года назад

5. Лише числівники записано в рядку А сім, сімка, семеро Б вісім, восьмеро, восьмий в дев'ять, дев'ятеро, дев'ятка г сорок, чверть, шістнадцятий...

Математика, 8 лет назад

2км 156м сколько км?

Математика, 8 лет назад

Цену товара увеличили на 28% найдите , сколько процентов составляет повышение цены.