Складіть рівняння кола з центром на бісектрисі другого координатного кута і радіусом 10, яке проходить через точку N(0;2)

Відповідь:

(х+8)²+(у-8)²=100.

Пояснення:

рівняння кола

(х-а)²+(у-b)²=R², де (а;b)-центр кола, R-радіус кола.

За умовою R=10, точка N(0;2) належить колу. Якщо центр кола належить бісектрисі другого координатного кута, тоді a<0, b>0. |a|=|b|

(0-a)²+(2-b)²=100,

b²+4-4b+b²=100

2b²-4b-96=0 |: 2,

b²-2b-48=0,

за теоремою Вієта b=-6, b=8.

b=-6, тоді а=6, що не відповідає умові;

b=8, тоді а=-8.

Рівняння кола:

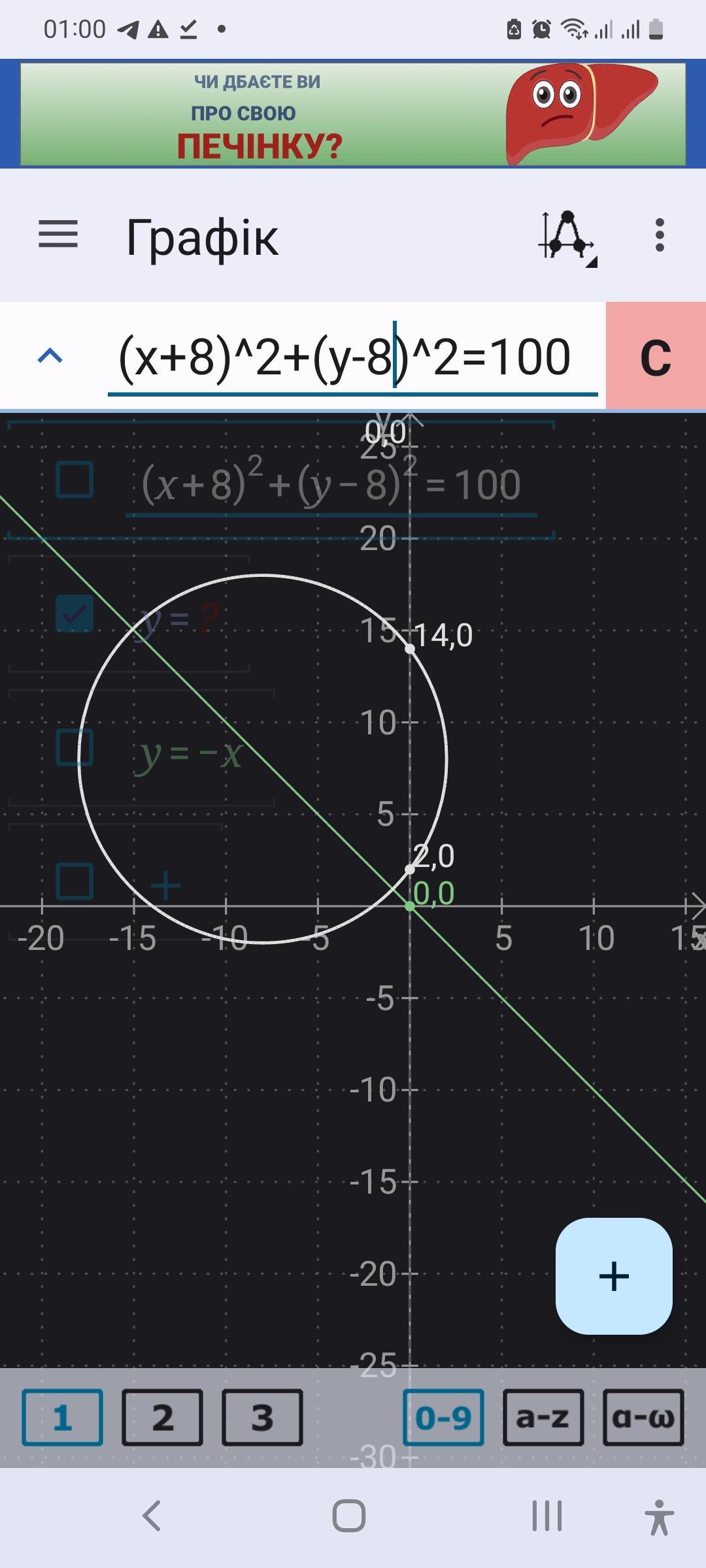
(х+8)²+(у-8)²=100.

Графіки рівняннь для демонстрації.