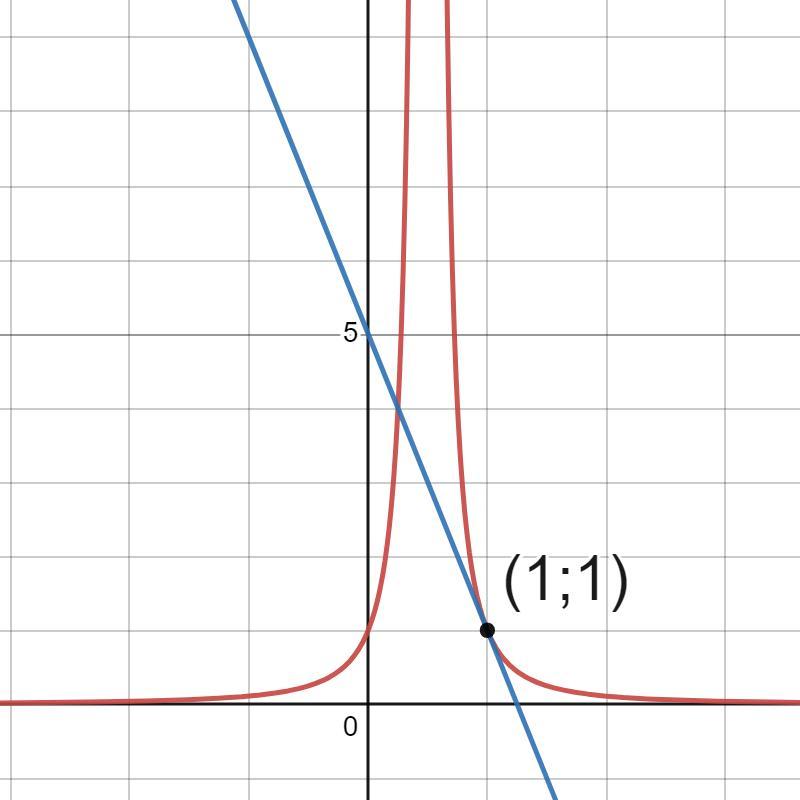
Алгебра, вопрос задал Lilya12062005 , 1 год назад

складіть рівняння дотичної до графіка функції f(x) в точці х0: f(x)=1/(2x-1)^2, x0=1

Ответы на вопрос

Ответил sangers1959

Пояснення:

$\displaystyle\\f(x)=\frac{1}{(2x-1)^2} \ \ \ \ \ \ x_0=1\ \ \ \ \ \ y_k=?\\\\$

$\displaystyle\\\boxed {y_k=f(x_0)+f'(x_0)*(x-x_0)}$

$\displaystyle\\f(1)=\frac{1}{(2*1-1)^2} =\frac{1}{(2-1)^2} =\frac{1}{1^2}=1.\\\\f'(x)=(\frac{1}{(2x-1)^2})'=((2x-1)^{-2})' =-2*(2x-1)^{-3}*(2x-1)'=-\frac{4}{(2x-1)^3} .\\\\f'(1)=-\frac{4}{(2*1-1)^3} =-\frac{4}{1}=-4.\\\\y_k=1+(-4)*(x-1)=1-4x+4=-4x+5.\\\\y_k=-4x+5.$

Відповідь: yk=-4x+5.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

История, 11 месяцев назад

Зерттеу сұрағы:Қазақ КСР-індегі ядролықсынақтардың қандай салдары болды??

Математика, 11 месяцев назад

1)2 кластың 78бірлігі және 1 кластың 820 бірлігінен тұратын сан 2)Төртінші разрядтың 2 бірлігі,үшінші разрядтың 8бірлігі және бірінші рязряд 5 бірлігінен тұратын сан #2. 36м²= 7215м= Пж көмек...

Геометрия, 1 год назад

СРОЧНО ДАЮ 100 БАЛЛОВ!!! сторона ромба утворює з його діагоналями кути, різниця яких 20 градусів. Знайдіть ці кути. Обов'язково з малюнком...

Алгебра, 1 год назад

5. Решите неравенство: x² (1 -x) < x²-4x+4 S0...

Українська література, 6 лет назад

Улюбленим композитором О. Кобилянської був:...

Математика, 6 лет назад

Здраствуйте помогите пожплуйста срочно 7-8 решать...