Математика, вопрос задал kochetovaleshcka , 1 год назад

Сириус задача срочно!
В каждой вершине куба написано целое число. За один ход к двум числам, написанным на концах некоторого ребра, можно прибавить по 1. Из каких начальных расстановок можно получить 8 равных чисел?

Приложения:

Ответы на вопрос

Ответил Guerrino

1) Рассмотрим квадрат. Пусть в его вершинах стоят числа $a,b,c,d$ (см.рис.)

Для любого такого квадрата введем величину: $I=(c-b)-(d-a)$ . Видно, что она постоянна при указанных действиях (добавление 1 к числам на ребре).

2) Очевидно, что последовательность действий не влияет на конечный результат. Поэтому пусть сначала действия производятся внутри верхних и нижних квадратов, а затем на ребрах (в данном случае вертикальных), которые эти квадраты соединяют. Пусть нам удалось получить куб с 8 равными числами. Пусть были сделаны все действия в квадратах. Тогда числа на вертикальных ребрах равны — иначе их не уравнять (мы сохраняем разность чисел). Если все числа на ребрах равны, то достаточно просто применить нужное количество операций к этим ребрам, чтобы получить все равные числа. Итак, наша задача имеет решение тогда и только тогда, когда один квадрат возможно перевести в другой. А эта задача, в свою очередь, имеет решение тогда и только тогда, когда величина $I$ для них совпадает.

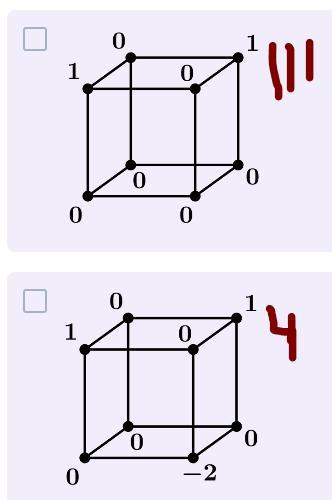
3) Рассматриваем первый куб: верхний квадрат: $I_{u}=(0-1)-(1-0)=-2$ , нижний $I_{d}=(0-0)-(0-0)=0$ , $I_{d}\neq I_{u}$ — задача решения не имеет.

Второй: верхний квадрат $I_{u}=(0-1)-(1-0)=-2$ , нижний — $I_{d}=(-2-0)-(0-0)=-2$ ; $I_{d}=I_{u}$ — задача имеет решение. Привести пример просто. Вот на словах: применяем операцию к ребру (-2, 0) и (0, -2). Имеем два равных квадрата. Дальше очевидно.

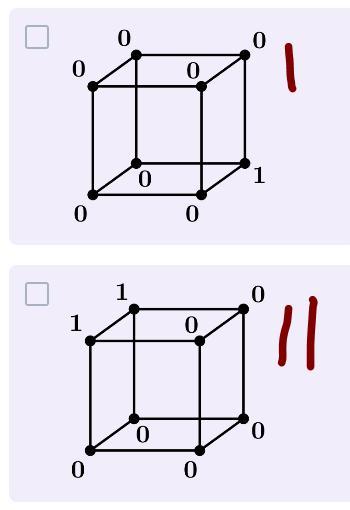
Третий: сумма чисел нечетна, сразу можно сказать нет.

Четвертый: применяем операцию к ребру под ребром (1, 1). Два равных квадрата. Дальше очевидно.

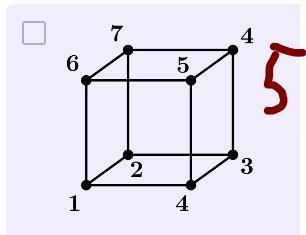
Пятый: $I_{u}=(5-4)-(6-7)=2$ , $I_{d}=(4-3)-(1-2)=2$ . Так что можно. Операция проста: производим действие над ребром (1, 2) 5 раз, над ребром (4, 3) один раз.