Сделать анализ графика на отрезке (с использованием производной)
Приложения:
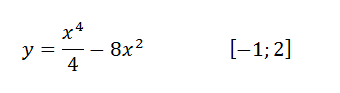
Ответы на вопрос
Ответил kalbim
0
1)
Производная положительная (функция возрастает): x∈(-4;0)U(4;+бесконечность)
Производная отрицательная (функция убывает): x∈(-бесконечность; -4)U(0;4)
На отрезке x∈[-1;2] функция и возрастает, и убывает. Т.е. при x∈[-1;0] - возрастает, а при x∈[0;2] - убывает.
Имеет максимум х=0,
2) Значения функции на концах отрезка:
Новые вопросы