Физика, вопрос задал sashakro008 , 1 год назад

С решением, ОЧЕНЬ НАДО, ПОЖАААААЛУЙСТА

Приложения:

Amalgamma143: Ты знаешь что такое векторное произведение?

Ответы на вопрос

Ответил Amalgamma143

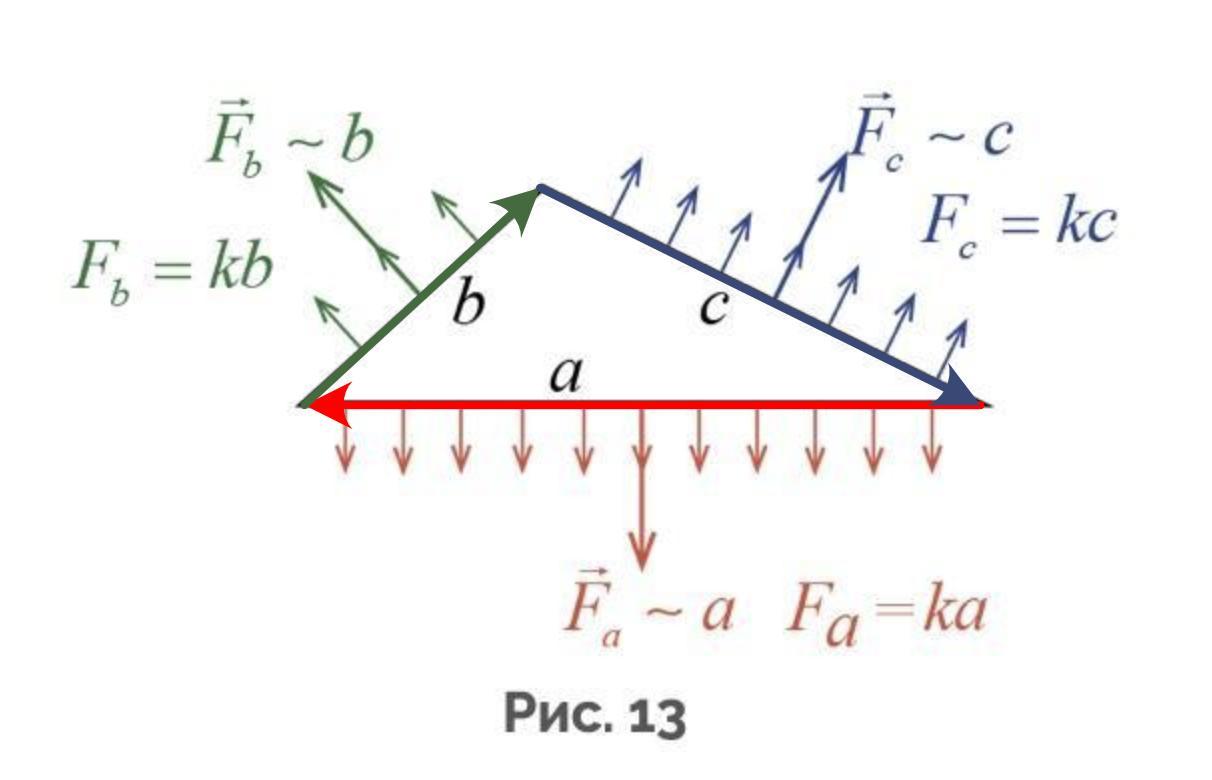
Введем векторы $\vec{a},\vec{b},\vec{c}$ как показано на прикрепленном рисунке

Тогда силы, приложенные к сторонам треугольника можно красиво записать при помощи векторного произведения

$\vec{F}_a = k[\vec{e}_z\times\vec{a}]\\\vec{F}_b = k[\vec{e}_z\times\vec{b}]\\\vec{F}_c = k[\vec{e}_z\times\vec{c}]$

Где $\vec{e}_z$ - единичный вектор, направленный на нас. Обратим внимание, что записанные таким образом силы удовлетворяют как условию пропорциональности (сила пропорциональна длине стороны), так и перпендикулярности, и направления сил тоже оказываются правильными, при правильном выборе векторов $\vec{a},\vec{b},\vec{c}$ как показано на прикрепленном рисунке

Поэтому векторная сумма всех сил

$\vec{F} = \vec{F}_a+\vec{F}_b+\vec{F}_c = k[\vec{e}_z\times(\vec{a}+\vec{b}+\vec{c})]=0$

Так как сумма трех указанных векторов равна нулю по правилу треугольника. Значит центр масс листочка двигаться не будет.

Чтобы понять, будет ли он вращаться, посчитаем момент приложенных к листочку сил. Так как центр масс листочка не ускоряется, мы вольны считать эту сумму относительно какой хотим точки, пускай относительно левой нижней вершины.

Тогда
$\vec{M}_a = [(-\vec{a}/2)\times\vec{F}_a] = -0.5k[\vec{a}\times[\vec{e}_z\times\vec{a}]] = -0.5ka^2\vec{e}_z$

$\vec{M}_b = [(\vec{b}/2)\times\vec{F}_a] = 0.5k[\vec{b}\times[\vec{e}_z\times\vec{b}]] = 0.5kb^2\vec{e}_z$

$\vec{M}_c = [(\vec{b}+\vec{c}/2)\times\vec{F}_c] = k[(\vec{b}+\vec{c}/2)\times[\vec{e}_z\times \vec{c}]] = k((\vec{b}\vec{c})+0.5c^2)\vec{e}_z$

и суммарный момент сил

$\vec{M} = 0.5k(c^2+b^2+2(\vec{b}\vec{c})-a^2)\vec{e}_z = 0.5k((\vec{b}+\vec{c})^2-a^2)\vec{e}_z = 0.5k(a^2-a^2)\vec{e}_z=0$

Сумма моментов оказалась равна нулю, и так как центр масс листочка не ускоряется, относительно любой другой точки эта сумма также будет равна нулю, что означает что листочек не вращается.

Ответ: не двигается и не вращается

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 11 месяцев назад

задание восемь! помогите срочно сейчас надооо...

Биология, 11 месяцев назад

16. Проаналізуй твердження щодо об'єкта (див. світлину) і вибери правильні. I на світлині зображено фрагмент м'язової тканини II - клітини м'язової тканини мають відростки, якими сполучають- ся...

Литература, 1 год назад

где и когда происходила Седьмое путешествие Синдбада...

Биология, 1 год назад

Визначити кількість темедійних нуклеотидів в днк, яка містить 14% цитозинових нуклеотидів...

Химия, 6 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА!Не проходите мимо!Вопрос по химии.5. зимой в центре внутренних рам окна ставят сосуд с концентрированной серной кислотой. Емкость с кислотой нельзя заполнять. Объясни причину!

Геометрия, 6 лет назад

обчислити всі невідомі кути трикутника...