С решением, логарифмы, нужна помощь!!
Приложения:

Ответы на вопрос
Ответил karasikov
0
одз: x - 2 > 0; 5 - x > 0; 2 < x < 5; x - 2 == 1; 5 - x == 1; x == 3, 4.
-x^2 + 7x - 10 > 0; -(x - 2)(x - 5) > 0; => x ∈ (2; 5) {3, 4}.
x^2 - 10x + 25 = (x - 5)^2;
0.5log(x - 2)_(x^2 - 10x + 25) = log(x - 2)_|x - 5| = log(x - 2)_(5 - x), тк x < 5;
log(5 - x)_(-x^2 + 7x - 10) = log(5 - x)_((5 - x) * (x - 2)) = 1 + log(5 - x)_(x - 2);
Пусть t = log(x - 2)_(5 - x)
Рассмотрим когда t > 0:
log(x - 2)_(5 - x) > 0;
(x - 2 - 1) * (5 - x - 1) > 0;
(x - 3) * (4 - x) > 0;
t > 0 при x ∈ (3; 4);
1)t < 0;
t + 1 + 1/t >= 3;
t^2 - 2t + 1 <= 0;
(t - 1)^2 <= 0;
t = 1;
log(x - 2)_(5 - x) = 1;
x - 2 = 5 - x;
2x = 7;
x = 3.5;
2) t > 0;
t + 1 + 1/t >= 3;
t^2 - 2t + 1 >= 0;
(t - 1)^2 >= 0;
При любом t > 0, т.е. x ∈ (3; 4);
3) t == 0, тк x == 4;
Ответ: x ∈ (3; 4).
-x^2 + 7x - 10 > 0; -(x - 2)(x - 5) > 0; => x ∈ (2; 5) {3, 4}.
x^2 - 10x + 25 = (x - 5)^2;
0.5log(x - 2)_(x^2 - 10x + 25) = log(x - 2)_|x - 5| = log(x - 2)_(5 - x), тк x < 5;
log(5 - x)_(-x^2 + 7x - 10) = log(5 - x)_((5 - x) * (x - 2)) = 1 + log(5 - x)_(x - 2);
Пусть t = log(x - 2)_(5 - x)
Рассмотрим когда t > 0:
log(x - 2)_(5 - x) > 0;
(x - 2 - 1) * (5 - x - 1) > 0;
(x - 3) * (4 - x) > 0;
t > 0 при x ∈ (3; 4);
1)t < 0;
t + 1 + 1/t >= 3;
t^2 - 2t + 1 <= 0;
(t - 1)^2 <= 0;
t = 1;
log(x - 2)_(5 - x) = 1;
x - 2 = 5 - x;
2x = 7;
x = 3.5;
2) t > 0;
t + 1 + 1/t >= 3;
t^2 - 2t + 1 >= 0;
(t - 1)^2 >= 0;
При любом t > 0, т.е. x ∈ (3; 4);
3) t == 0, тк x == 4;
Ответ: x ∈ (3; 4).
Приложения:
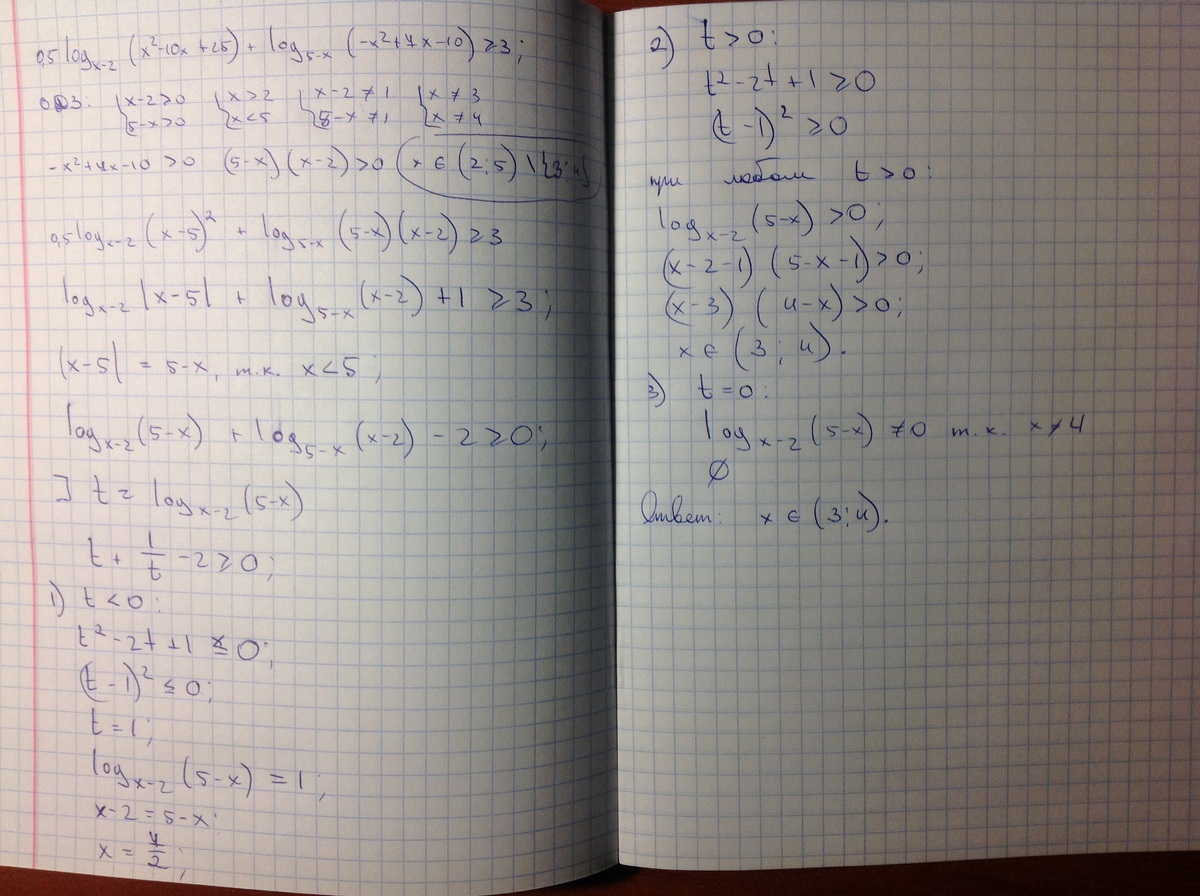
Новые вопросы