Розвяжіть будь-ласка то что на фото.
Приложения:
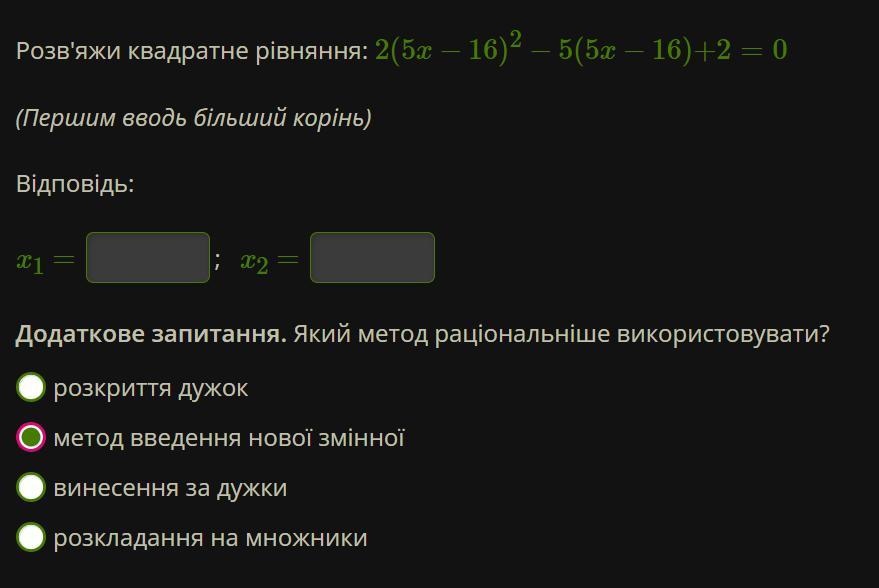
xokyno:
x1=3.6 x2=3.3 розкл. на множн.
Ответы на вопрос
Ответил сок111213
0
Ответ: 3,3 и 3,6 ; метод введения новой переменной
Ответил iramazurk
0
Ответ:
3,6; 3,3
Объяснение:
2(5х - 16)² - 5(5х - 16) + 2 = 0
Пусть: 5х - 16 = t
2t² - 5t + 2 = 0
а = 2; в = -5; с = 2
Д = в² - 4ас
Д = (-5)² - 4 * 2 * 2 = 25 - 16 = 9
√Д = √9 = 3
t1 = (-в + √Д)/2а
t1 = (5 + 3)/(2*2) = 8/4 = 2
t2 = (-в - √Д)/2а
t2 = (5 - 3)/(2*2) = 2/4 = 1/2 = 0,5
1)
5х - 16 = 2
5х = 2 + 16
5х = 18
х = 18 : 5
х1 = 3,6
2)
5х - 16 = 0,5
5х = 0,5 + 16
5х = 16,5
х = 16,5 : 5
х2 = 3,3
Дополнительный вопрос:
рациональней использовать: метод введения новой переменной.
Новые вопросы
Қазақ тiлi,
11 месяцев назад
Українська література,
11 месяцев назад
Английский язык,
1 год назад
Геометрия,
1 год назад
Обществознание,
6 лет назад