Алгебра, вопрос задал school2760 , 2 года назад

Розв'яжіть рівняння

Приложения:

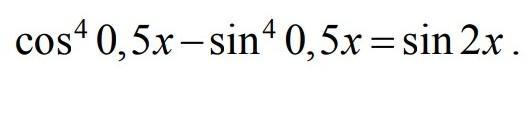
Ответы на вопрос

Ответил SpringScorpion

3

Ответ:

$x_{1} = \frac{\pi}{6} + \frac {2k\pi}{3} \: \: k \in Z \\ \\ x_{2} = \frac{\pi}{2} + k\pi \: \: k \in Z$

Объяснение:

$cos(0.5x)^{4} - sin(0.5x)^{4} = sin(2x) \\ \\ cos( \frac{1}{2} x)^{4} - sin( \frac{1}{2} x)^{4} = sin(2x) \\ \\ (cos( \frac{1}{2} x)^{2} - sin( \frac{1}{2} x)^{2} ) \times (cos( \frac{1}{2} x)^{2} + sin( \frac{1}{2} x)^{2} ) = sin(2x) \\ \\ cos(x) \times 1 = sin(2x) \\ \\ cos(x) = sin(2x) \\ \\ cos(x) - sin(2x) = 0 \\ \\ cos(x) - 2sin(x)cos(x) = 0 \\ \\ cos(x) \times (1 - 2sin(x)) = 0$

Тогда имеем 2 уравнения —

cos(x) = 0
1 - 2sin(x) = 0

Решаем —

$x_{1} = \frac{\pi}{2} + 2k\pi \: \: k \in Z \\ \\ x_{2} = \frac{\pi}{6} + 2k\pi \: \: k \in Z \\ \\ x_{3} = \frac{5\pi}{6} + 2k\pi \: \: k \: \in Z$

Находим объединение —

$x_{1} = \frac{\pi}{6} + \frac {2k\pi}{3} \: \: k \in Z \\ \\ x_{2} = \frac{\pi}{2} + k\pi \: \: k \in Z$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Выписать !ПРИЧАСТИЯ! из текста Каштанка съела много, но не наелась, а только опьянела от еды. (2)После обеда она разлеглась среди комнаты, протянула ноги и, чувствуя во всем теле приятную истому,...

Русский язык, 1 год назад

помогите пожалуйста написать сочинение...по этим картинкам...

Информатика, 2 года назад

Известно, что Х - натуральное число из интервала от 7 до 38 включительно. Имеются два высказывания о числе Х: A = {X > 17} B = {X > 21} Какое из перечисленных ниже высказываний несёт...

Другие предметы, 2 года назад

сауатты синоним антоним...

История, 7 лет назад

Алтай в 13-15 веках (кратко)...

Биология, 7 лет назад

Напишите,почему необходимо давать организмам научные названия,а также классифицировать их.