Розв'яжіть нерівність: log3 (2x-1) + log3 (x-9) < 2

Відповідь:

Пояснення:

фото

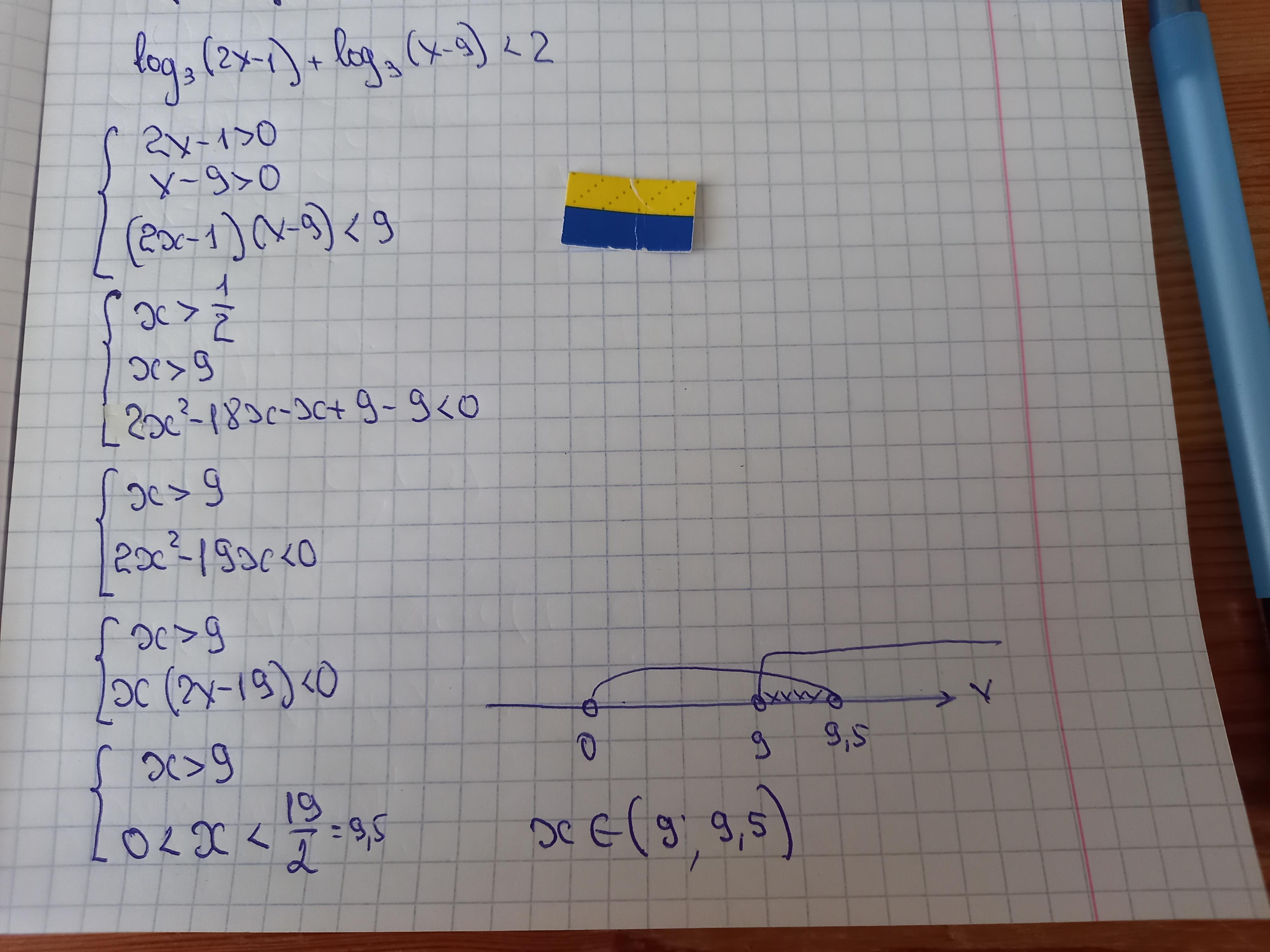
Для начала найдем область допустимых значений самих логарифмов. Мы знаем, что выражение, находящееся под знаком логарифма, всегда должно быть положительным. Тогда:

Объединением этих двух промежутков является   , или , значит, это и будет областью допустимых значений.

Теперь перейдём к самому нашему неравенству и начнём упрощать его. По свойству логарифмов: .

Теперь раскроем скобку:

Теперь нам надо привести правую часть к логарифму с таким же основанием, что и в левой части. Мы знаем, что   . Подставим это в неравенство.

Теперь и в левой, и в правой части у нас стоят логарифмы с одинаковыми основаниями, и мы можем сравнить выражения под знаком логарифма. Но прежде обратим внимание на основание. Основание равно 3, что больше единицы, значит, знак неравенства не меняется.

Для начала найдем значения, при которых множители в левой части обратятся в ноль. С первым множителем всё просто, получаем  , а теперь найдём ноль второго множителя.

Решим неравенство методом интервалов.

             +                              -                                +

--------------------------о--------------------------о-------------------------->

Так как неравенство имеет знак "меньше", то нам надо выбрать те промежутки, где стоит знак "минус". Такой только один: . Но не забываем про найденную нами в самом начале область определения, согласно которой наш не может быть меньше, чем 9. Таким образом, наша левая граница сдвигается к 9, а правая остаётся такой же. И получаем финальный ответ: .

Ответ: .