Математика, вопрос задал shnyrokt , 6 месяцев назад

Розв'язати інтеграл, даю 85 балів

Приложения:

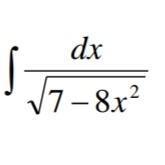
Ответы на вопрос

Ответил polarkat

$$\int \frac{dx}{\sqrt{7-8x^2}}=\frac{1}{\sqrt{7}}\int \frac{dx}{\sqrt{1-8x^2/7}}\overset{u=2\sqrt{2/7}x}{=}\frac{1}{2\sqrt{2}}\int \frac{du}{\sqrt{1-u^2}}=$\\$ $=\frac{\mathrm{arcsin}\; u}{2\sqrt{2}}+C=\frac{1}{2\sqrt{2}}\mathrm{arcsin}\left ( 2\sqrt{\frac{2}{7}}x \right )$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 4 месяца назад

Помогите пожалуйста решить уравнение Сторона ВС треугольника АВС параллельна плоскости В, а стороны АВ и АС пересекают плоскость в точках М и N соответственно. 1) Докажите, что ДАММ ДАВС. 2) Найдите...

Геометрия, 4 месяца назад

Знайдіть градусну міру кута ∠...

Физика, 6 месяцев назад

7. Камертон випромінює звукову хвилю частотою 64 Гц. Швидкість звуку 340 м/с. Яка довжина хвилі звукової хвилі створеної камертоном?

Русский язык, 6 месяцев назад

Прочитайте предложения, взятые из классических произведений, и проанализируйте употребление существительных в единственном и множественном числе. Когда эти формы реально указывают на один и много...

Биология, 6 лет назад

Кто из ниже перечисленных относится к отряду однопроходные? а. Мышь; б. Кенгуру; в. Крот; г. Ехидна...

Литература, 6 лет назад

рассказ ( воспоминание ) жука носорога о его боевом пути...