Математика, вопрос задал zoriana1254 , 6 лет назад

розв'язати нерівність

Приложения:

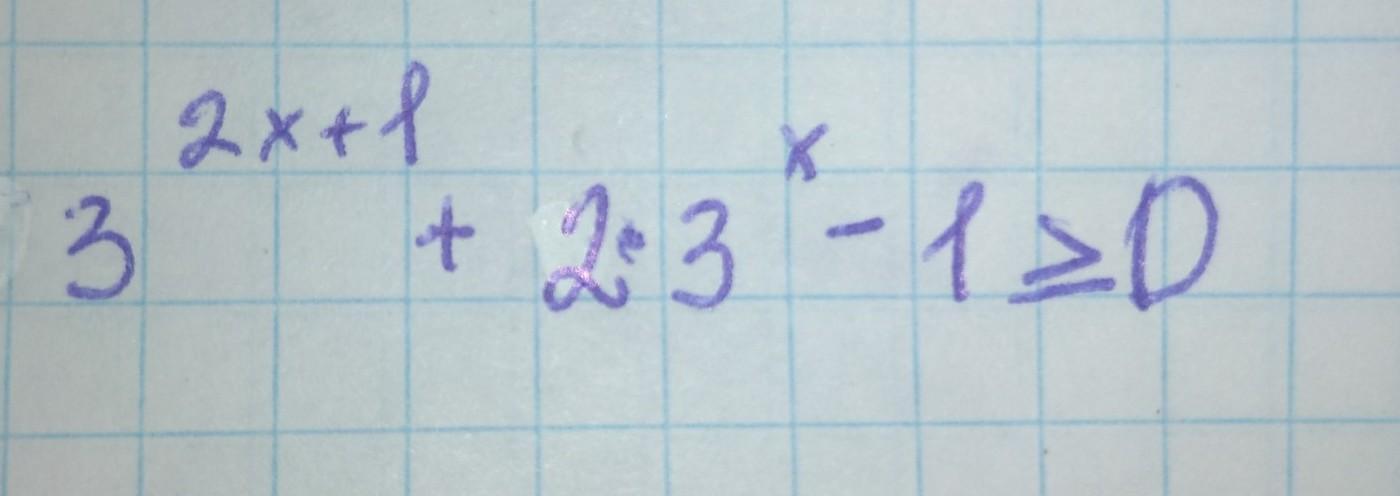
Ответы на вопрос

Ответил zinaidazina

1

$3^{2x+1}+2*3^{x}-1\geq 0$

$3^{2x}*3^1+2*3^{x}-1\geq 0$

$3*(3^{x})^2+2*3^{x}-1\geq 0$

Замена:

$3^x=t$ (ОДЗ: $t>0$ )

$3t^2+2t-1\geq 0$

$3(t-\frac{1}{3} )(t+1)\geq 0$

+ - +

///////////,______________///////////////////////

$-1$ $\frac{1}{3}$

$t\leq -1$ $t\geq \frac{1}{3}$

$t\leq -1$ не удовлетворяет ОДЗ.

$t\geq \frac{1}{3}$ удовлетворяет ОДЗ.

Замена:

$t\geq \frac{1}{3}$ => $3^x\geq \frac{1}{3}$

$3^x\geq 3^{-1}$

Так как $3>1$ , то $x\geq -1$

Ответ: $[-1;+ \infty} )$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Физика, 1 год назад

Закончить атомные реакции по физики...

Английский язык, 1 год назад

Помогите пожалуйста.Необходимо сделать 1,3,4 задания.

Русский язык, 6 лет назад

Какой род у слова белка?

Русский язык, 6 лет назад

Помогите пожалуйста с этим заданием я его не поняла. Прочитайте текст. Запишите своими словами информацию, которую вы хотели бы для себя выделить. Русский язык-один из богатейших языков мира. К.

Алгебра, 8 лет назад

Можете помочь пожалуйста срочно надо!!!

Информатика, 8 лет назад

С:=sqrt(d); Какого типа должна быть переменная С для данного выражения?