Алгебра, вопрос задал ivkalieva , 11 месяцев назад

Розвʼязати графік функції,з поясненням та розвʼязком

Приложения:

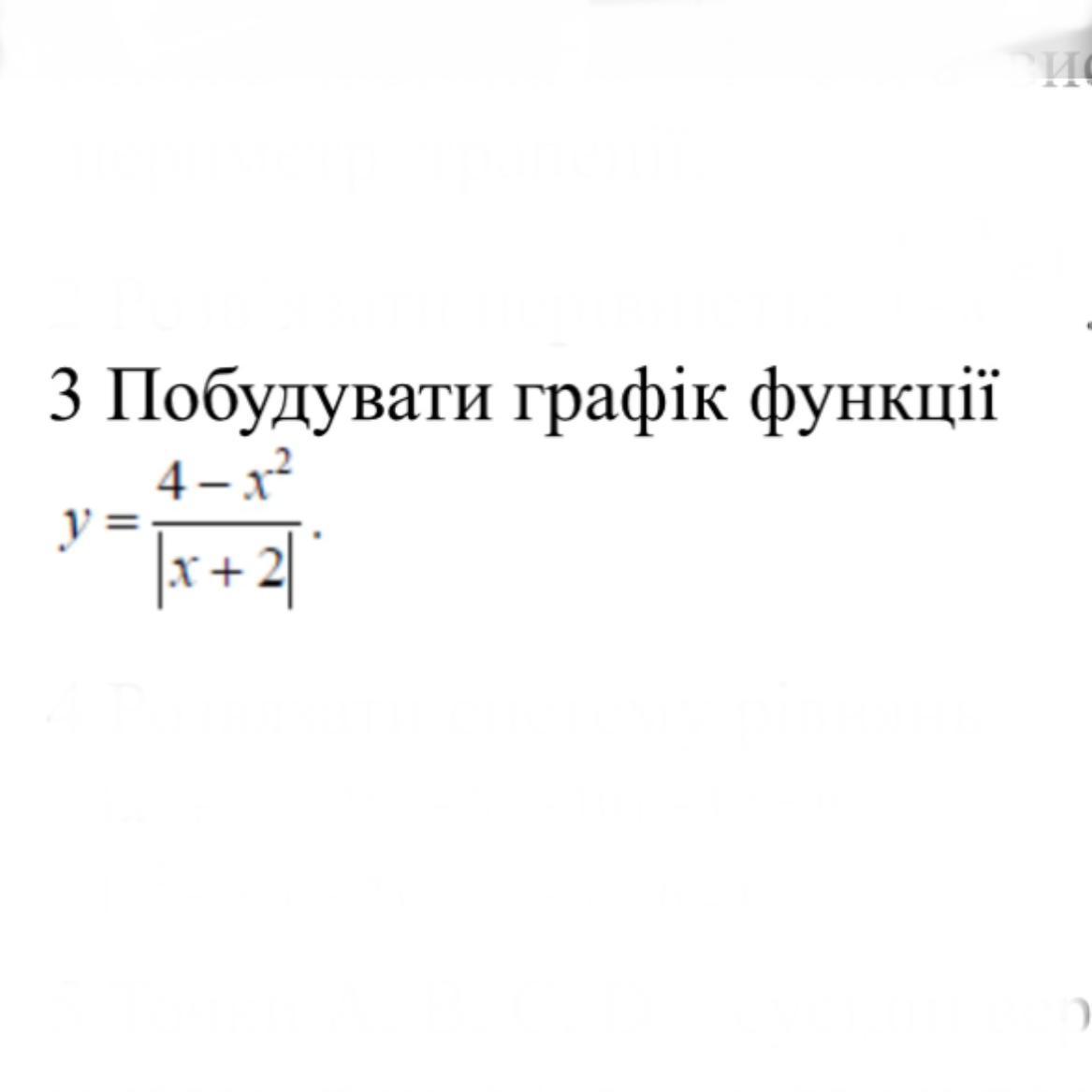
Ответы на вопрос

Ответил 7x8

Ответ:

на фото

Объяснение:

$y=\frac{4-x^2}{|x+2|}$

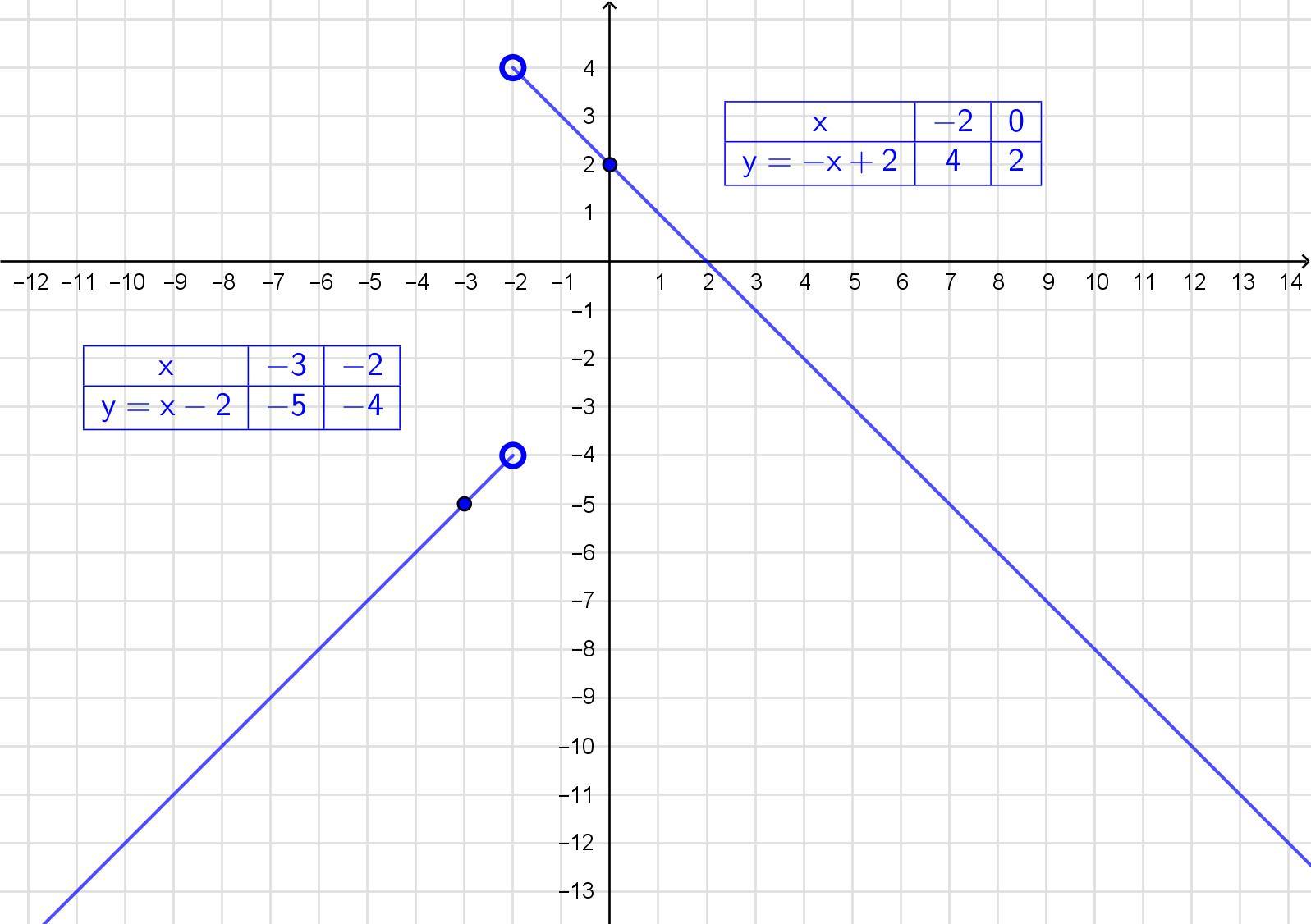
ОДЗ:

$x \neq -2$

$x<-2$

функція набуває вигляду

$y=\frac{4-x^2}{-(x+2)}=\frac{(2-x)(2+x)}{-(x+2)}=\frac{2-x}{-1}=-2+x=x-2$

$x>-2$

функція набуває вигляду

$y=\frac{4-x^2}{x+2}=\frac{(2-x)(2+x)}{x+2}=\frac{2-x}{1}=2-x=-x+2$

$y=\begin{cases}x-2\ \ \ \ \ \ \ \ x<-2\\-x+2\ \ \ \ \ x>-2\end{cases}$

(-2;-4), (-2,4) - крапка виколота (незакрашена)

Приложения:

ivkalieva: Дякую!!!

7x8: :)

ivkalieva: Можеш ще одне розвʼязати?Дам 20 балів,зараз створю завдання

Новые вопросы

Українська мова, 11 месяцев назад

Геометрия, 11 месяцев назад

Литература, 11 месяцев назад

Русский язык, 11 месяцев назад

Русский язык, 6 лет назад

Английский язык, 6 лет назад