Розкласти многочлен на множники (виконати ділення многочлена кутом).
Приложения:
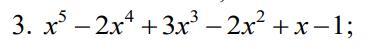
Ответы на вопрос
Ответил natalyabryukhova
1
Ответ:
x⁵ - 2x⁴ + x³ - 2x² + x - 1 = (х - 1)(х⁴ - х³ + 2х²+1)
Объяснение:
Разложить многочлен на множители (выполнить деление многочлена углом).
x⁵ - 2x⁴ + x³ - 2x² + x - 1
Для решения воспользуемся следствием теоремы Безу.
Если дан многочлен с целыми коэффициентами и один из его корней х₁, то свободный член будет нацело делиться на этот корень.
В данном многочлене свободный член равен 1.
Проверим, является ли 1 корнем многочлена:
1 - 2·1 + 3·1 - 2·1 +1 - 1 = 0
⇒ 1 - один из корней нашего многочлена.
Тогда Р(х) = (х - х₁) Q(x)
Разделим столбиком данный многочлен на (х - 1)
См. вложение.
Получим:
x⁵ - 2x⁴ + x³ - 2x² + x - 1 = (х - 1)(х⁴ - х³ + 2х²+1)
Приложения:
fctdgsygfdhngfxzgsac:
спасибо большое))
natalyabryukhova, спасибо большое что помогли, можете еще помочь пожалуйста? с етим заданием https://znanija.com/task/54251112
Новые вопросы
Геометрия,
11 месяцев назад
Українська література,
11 месяцев назад
Литература,
11 месяцев назад
Физика,
11 месяцев назад
Алгебра,
6 лет назад